Решение. Рассмотрим сечение, состоящее из прокатных профилей (см

Рис.1

Пример 12.

Рассмотрим сечение, состоящее из прокатных профилей (см. рис.1).

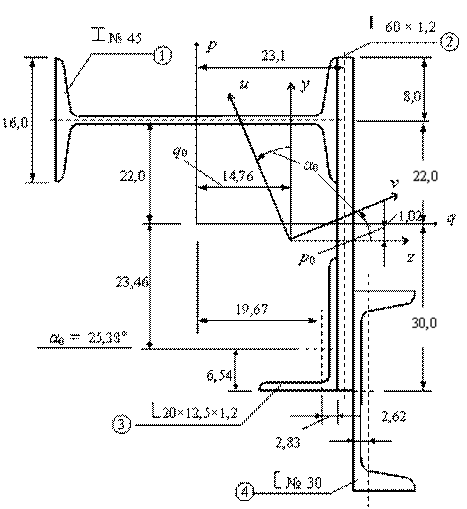
Вычертив в масштабе сечение, нумеруем элементы, с указанием их размерных характеристик – номера двутавра и швеллера, размеры перьев и толщину уголков, высоту и толщину листа.

Проставляем начальные размеры, необходимые для определения положения элементов в сечении – ширина полки двутавра, расстояния до центров тяжестей уголка и швеллера от их граней (из таблицы ГОСТ).

Принимаем положение начальных осей сечения. Пусть горизонтальная ось q проходит через центр тяжести вертикального листа, а вертикальная р – через центр тяжести двутавра. Указываем на чертеже положение начальных осей.

Рассчитываем и указываем на чертеже координаты центров тяжести элементов относительно начальных осей.

р_с = -1,02 см; q_c = 14,76 см.

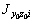Определяем осевые , и центробежный моменты инерции элементов относительно собственных центральных осей параллельных начальным осям сечения. Осевые моменты инерции двутавра, швеллера и уголков принимается из таблиц ГОСТ, с учетом положения их осей. Осевые моменты инерции листа (прямоугольное сечение) рассчитываются по формуле 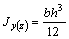, где b - размер параллельный, h – размер перпендикулярный оси, относительно которой вычисляется момент инерции.

Для вертикального листа 60´1,2 (см) (элемент № 2) имеем:

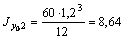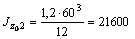см4; см4.

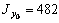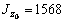Центробежный момент инерции в рассматриваемом сечении отличен от нуля только у неравнобокого уголка (элемент № 3). Согласно ГОСТ 8210-86 для неравнобокого уголка - 20´12,5´1 см⁴; см ⁴; 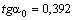. Согласно рис. 2 угол .

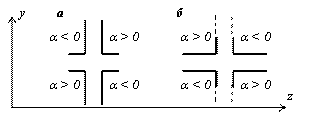
Рис.2. К определению знака угла положения главных осей уголков

Тогда по формуле 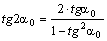получим и по формуле 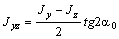: 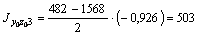см⁴.

Все данные по элементам сечения - моменты инерции относительно центральных осей элементов и координаты центров тяжестей заносятся в таблицу (см. табл.). Табличная форма позволяет удобно контролировать правильность подготовки исходных данных, от которых зависит корректность дальнейших расчетов.

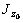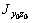№ п/п	Тип элемента	А, см^2	, cм^4	, cм^4	, cм^4	pc , см	qc , см	yc, см	zc, см
1.	I № 45	84,7				22,0		23,02	-14,76
2.	| 60´1,2	72,0	8,64				23,10	1,02	8,34
3.	ë20´12,5´1,2	37,9				-23,46	19,67	-22,44	4,91
4.	[ № 30	40,5				-30,00	26,22	- 28,98	11,46
		235,1

Вычисляем координаты центра тяжести сечения относительно начальных осей:

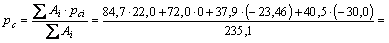
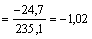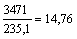см;

см.

7. Определяем координаты центров тяжести элементов сече ния относительно центральных осей:

; ;

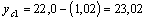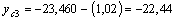см; см;

см; см;

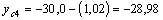см; см;

см; см.

Координаты центров тяжестей элементов записываем в таблицу.

Проводим проверку правильности вычисления координат центров тяжести сечения и его элементов:

; ;

=.

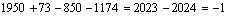Относительная невязка:

;

.

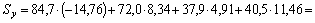
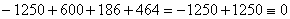Определяем осевые, центробежный и полярный моменты инерции сечения относительно центральных осей:

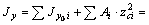
см ⁴;

см ⁴;

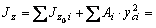
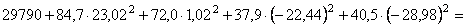
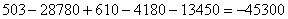см⁴;

см⁴.

Замечание. Результаты расчетов округлялись до четырех значащих цифр.

Определяем положение главных осей:

; ; .

Определяем главные моменты инерции:

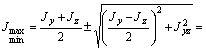
(см⁴);

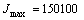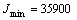см⁴; см⁴;

или, в соответствии с формулами:

; ;

;

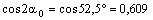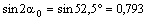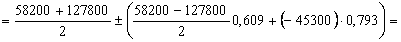
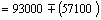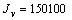см ⁴; см ⁴;

Из расчета видно, что 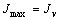, т.е. максимальный момент инерции возникает относительно оси v, которая ближе к оси z, оси с наибольшим значением момента инерции .

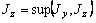Сумма главных моментов инерции должна быть равна сумме осевых моментов инерции, или полярному моменту инерции

.

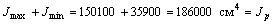Определение главных моментов инерции и положения главных осей с помощью круга Мора (рис. 3).

Дата добавления: 2013-12-13