Решение. Найти положение главных центральных осей инерции и значение главных моментов инерции для сечения состоящего из равнобокого уголка и двутавра (см

Пример 15.

Найти положение главных центральных осей инерции и значение главных моментов инерции для сечения состоящего из равнобокого уголка и двутавра (см. рис.1). Вычертить сечение в масштабе 1:2 и указать на нём все размеры в числах и все оси, если дано: уголок 90х7, двутавр №22.

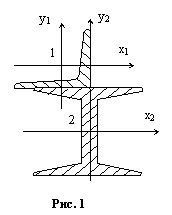
Из сортамента выбираем необходимые данные.

Для уголка равнобокого 90х7 по ГОСТ 8509-89 b = 90 мм, d = 7 мм, z₀ = 2,47 см, F₁=12,28 см², I_x1 = I_y1 = 94,3 см⁴, I_max = 149,67 см⁴, I_min = 38,94 см⁴.

Для двутавра по ГОСТ 8239-89 h = 220 мм, b = 110 мм,d =5,7 мм, F₂ = 30,6 см², I_x2 = 2550 см⁴, I_Y2 = 157 см⁴.

1. Проводим вспомогательную систему осей координат (Х, Y). Начало координат целесообразно расположить в центре тяжести какой-либо из фигур, напримердвутавра (чтобы сократить объём вычислений). Определяем координаты центра тяжести С всей фигуры в системе осей Х и Y:

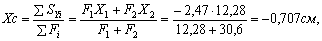
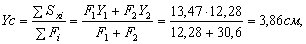
где

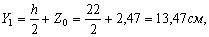
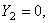
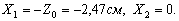
Через центр тяжести С (рисунок 3) проводим центральные оси Х_С и Y_C параллельно проведённым ранее собственным осям уголка и двутавра (Х₁, Y₁, Х₂, Y₂).

В системе координат центральных осей Х_С и Y_C координаты центров тяжести уголка и двутавра определяем из выражений

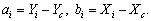
Данные сводим в таблицу 1.

Таблица 1

Точка	хi, см	yi, см	ai, см	bi, см
О1	- 2,47	13,47	9,61	- 1,76
О2			- 3,86	0,707

2. Вычисляем осевые и центробежный моменты инерции относительно центральных осей X_с, Y_с:

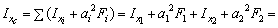
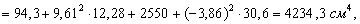
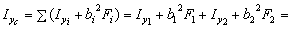
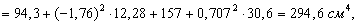
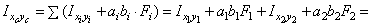
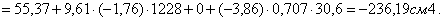
Для равнобокого уголка

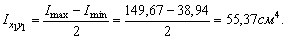
Для двутавра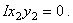

Знак центробежного момента инерции уголка определяем по следующему правилу (см. рис.2):

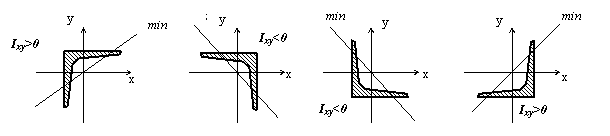
Дата добавления: 2013-12-13