Решение. Определить полярный момент инерции круглого поперечного сечения (см

Пример 14.

Пример 13.

Решение.

Пример 12.

Решение.

Пример 11.

Определить полярный момент инерции круглого поперечного сечения (см. рис.) относительно точки С.

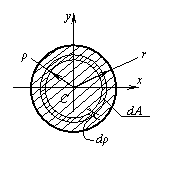
За элементарную площадку выберем кольцевую область вокруг центра С с внутренним радиусом ρ и шириной dρ. Определим площадь элементарной площадки 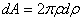. Затем результат подставляем в формулу :

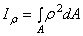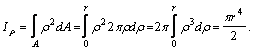
Определить осевые моменты инерции круглого сплошного поперечного сечения относительно произвольных центральных осей х, у (см. рис.).

В примере 17 найдено, что 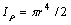. Однако для круглого сплошного сечения I_x = I_y, поэтому формула 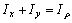для этого сечения принимает вид: 2 I_x = I_ρ, откуда находим

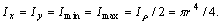
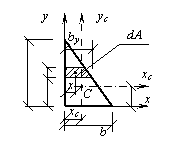
Определить осевые моменты инерции I_x, I_y прямоугольного треугольника относительно случайных осей х, у (см. рис.). Вычислить положение центра тяжести. Найти значения осевых моментов 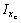инерции ,и центробежный момент инерции 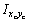относительно центральных осей х_с, у_с, проходящих через центр тяжести С. Определить расположение главных осей инерции поперечного сечения в форме сплошного прямоугольного треугольника.

Указания. Для нахождения центробежного момента инерции 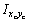можно использовать формулы 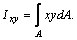и 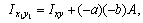которые для рассматриваемого случая принимают вид:

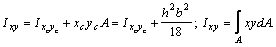
Из подобия треугольников находим (см. рис.): 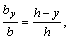откуда 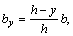следовательно, площадь элементарной площадки dA будет

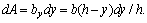
Горизонтальная координата х центра тяжести элементарной площадки dA определяется как x = b_y / 2 =b (h – y)/( 2 h).

Подставим значения х и dA в формулу для определения I_xy:

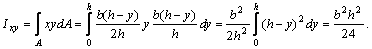
Переходим к центральным осям х_с и у_с, для которых

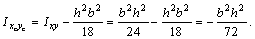
Ответ: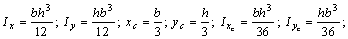

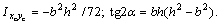
Определить расстояние а между элементами пакета, состоящего из трех досок размером 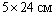, при условии равенства главных моментов инерции относительно осей х и у (см. рис.).

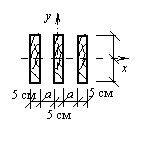
Момент инерции всего сечения относительно оси х будет

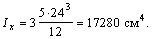
При определении момента инерции сечения относительно оси у для двух крайних прямоугольников следует воспользоваться формулой 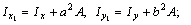так как ось у не является для них центральной и, следовательно, для всего пакета из трех досок будем иметь

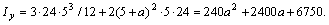
По условию задачи I_x = I_y, или 17280 = 240 a² + 2400 a + 6750.

Решив полученное квадратное уравнение, найдем a = 3,3 см.

Дата добавления: 2013-12-13