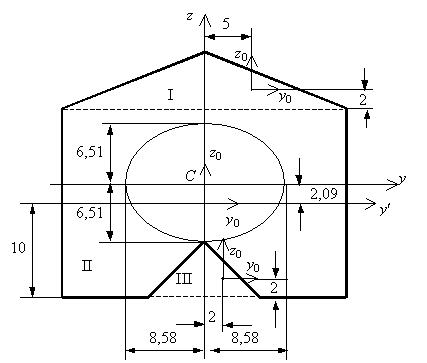
Решение. Сечение стержня представляющее собой фигуру, обладающую одной осью симметрии, показано на рис

Пример 16.

Рис.2

Решение.

Рис.1

Пример 15.

Сечение стержня представляющее собой фигуру, обладающую одной осью симметрии, показано на рис. 1. Требуется найти моменты инерции этой фигуры относительно главных центральных осей.

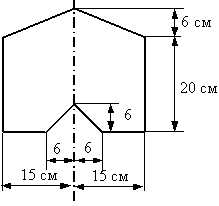
Ось – ось симметрии фигуры (рис. 1) является главной осью инерции. Найдем положение второй главной центральной оси, определив положение центра тяжести фигуры. Очевидно, что центр тяжести лежит на оси симметрии, поэтому найдем только координату 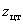по формуле 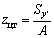. Разобьем сложную фигуру на составляющие простые: две пары прямоугольных треугольников I, III и прямоугольник II (см. рис. 2). Площадь фигуры

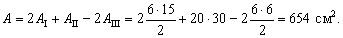
Для определения статического момента выберем вспомогательную ось 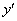, проходящую через центр тяжести прямоугольника II. В этом случае статический момент фигуры II равен нулю. Чтобы найти статические моменты треугольников, умножаем площадь фигуры на координату ее центра тяжести в системе :

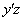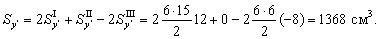
Тогда по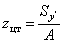

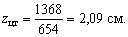
Откладываем эту координату и проводим через центр тяжести (точку С на рис. 2) главную центральную ось .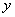

Найдем моменты инерции всей фигуры относительно осе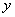й и , складывая (или вычитая) моменты инерции составляющих фигур:

;

.

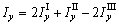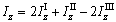Для определения момента инерции каждой из фигур I, II и Ш используем формулы изменения моментов инерций при параллельном переносе осей 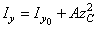, 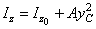. Моменты инерции прямоугольника II находим по формулам 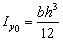; ; 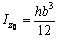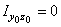и треугольников I и Ш находим по формулам ; ; 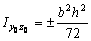относительно собственных центральных осей 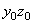(см. рис. 2).

Тогда

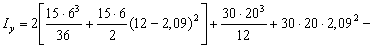
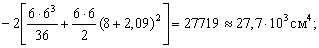
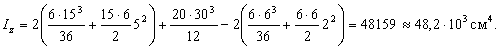
В заключение вычислим радиусы инерции относительно главных центральных осей по формулам 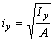, и построим эллипс инерции.

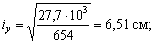
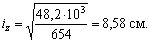
Эллипс инерции показан на рис. 2.

Для фигуры, показанной на рисунке определить главные моменты инерции и положение главных осей инерции.

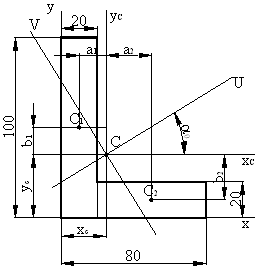
Разбиваем сложное сечение на простейшие геометрические фигуры

S₁ = 2000 мм², S₂ = 1200 мм², S = 3200 мм².

Выбираем произвольные оси XOY.

Определяем положение центра тяжести сечения

Определяем статические моменты площади

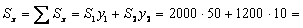
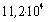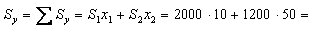
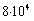мм³

мм³

Находим координаты центра тяжести

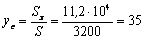мм;

мм.

Проводим центральные оси X_cOY_c

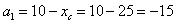мм,

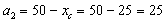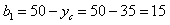мм,

мм,

мм.

Вычисляем моменты инерции Ix_c, Iy_c

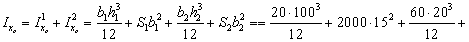
мм⁴

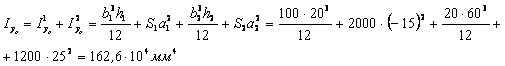
6) Вычисляем центробежный момент инерции Ix_cy_c

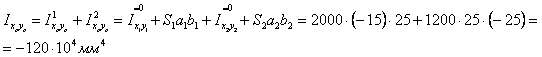
Определяем положение главных осей инерции

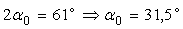
Если I_x>I_y и 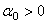, то угол откладывается от оси Х_с против часовой стрелки.

7) Вычисляем главные моменты инерции I_max, I_min

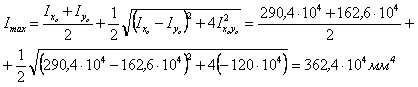
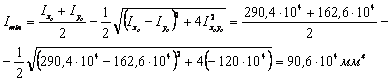
Дата добавления: 2013-12-13