IV квадрант – передний нижний

Проекции разделяются на центральные и параллельные.

Проекции точки.

Лекция 1

1. Методы проецирования.
2. Плоскости проекции.
3. Задание точки на комплексном чертеже Монжа (или эпюр Монжа).
4. Обратимость чертежа.

Предметом начертательной геометрии является изложение и обоснование способов построения изображений пространственных форм на плоскости и способов решения задач геометрического характера по заданным изображениям этих форм.

Изображения, построенные по правилам, изучаемым в начертательной геометрии, позволяют представить мысленно форму предметов и их взаимное расположение в пространстве, определить их размеры, исследовать геометрические свойства, присущие изображаемому предмету.

Начертательная геометрия передает часть своих выводов в практику выполнения технических чертежей, обеспечивая их выразительность и точность, а, следовательно, и возможность осуществления изображенных предметов.

1.1. Метод проецирования.

Для построения изображения предметов на плоскости пользуются методом проецирования. Слово «проекция» - латинское, от глагола projecere, что в переводе означает «бросать вперед».

Следовательно, проекция – это изображение предмета, «отброшенное» на плоскость при помощи лучей. Спроецировать предмет на плоскость – это значит построить его изображение на плоскости.

Рассмотрим центральное проецирование (рис. 1.1.).

Пусть заданы в пространстве точка S – центр проекции и плоскость П₁ – плоскость проекции. Плоскость П₁ и точка S составляют аппарат центральной проекции. Проецируемый треугольник АВС называется оригиналом, или натурой. Чтобы спроецировать заданный оригинал, нужно из центра проекции S через вершины треугольника провести проецирующие лучи до пересечения с плоскостью проекции П₁. Точки пересечения А₁, В₁, С₁, называются центральными проекциями вершин А, В, С, на плоскость П₁, а треугольник А₁В₁С₁ – центральной проекцией треугольника АВС.

Центральные проекции (перспективу) применяют в архитектурных чертежах, в аэрофотосъемке, рисовании и др. Вследствие трудностей при построении изображений и их измерении, а также при чтении чертежей, в машиностроительном черчении центральными проекциями не используются.

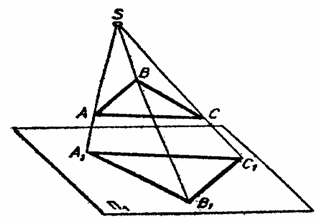
Рис. 1.1.

В начертательной геометрии используют метод параллельного проецирования (рис. 1.2.). Как и в предыдущем случае, выбирают плоскость проецирования П₁, но вместо центра проекции S задают направление проецирования s, т. е. считают, что точка S – центр проекции – расположена в бесконечности и поэтому проецирующие лучи параллельны между собой. Плоскость П₁ и направление s составляют аппарат параллельной проекции. Чтобы спроецировать треугольник АВС на плоскость П₁, через вершины А, В, С проводят проецирующие лучи параллельно направлению проецирования s. Треугольник А₁В₁С₁, образованный пересечением лучей АА₁, ВВ₁, СС₁ с плоскостью П₁, и будет параллельной проекцией треугольника АВС.

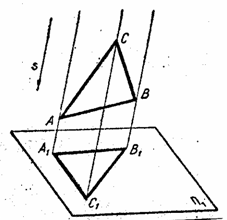
Рис. 1.2.

Параллельные проекции разделяются на прямоугольные и косоугольные. Если проецирующие лучи перпендикулярны к плоскости проекций (рис. 1.3.), то способ проецирования называется прямоугольным, а полученные при этом проекции – прямоугольными, или ортогональными.Если же угол наклона лучей не равен 90º, то подобная параллельная проекция называется косоугольной. В черчении используют, главным образом, прямоугольные проекции.

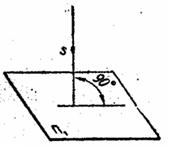
Рис. 1.3.

1.2 Пространственная (или декартовая) система координат. Плоскости проекций

В данном курсе будут рассмотрены чертежи, получаемые ортогональным проецированием на две или более взаимно перпендикулярные плоскости проекций (комплексный чертеж) и путем перепроецирования вспомогательной проекции предмета на основную аксонометрическую плоскость проекций (аксонометрический чертеж).

Из рис. 1.4 видно, что проекции А₁ отвечает бесчисленное множество точек (А, A’, A''), лежащих на проецирующем луче, идущем из А₁ перпендикулярно к плоскости проекции П₁.

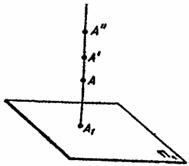
Рис. 1. 4.

Совокупность двух прямоугольных проекций на две взаимно перпендикулярные плоскости позволяет однозначно определить форму и положение предмета в пространстве. Однако в черчении при построении изображений чаще используют три плоскости проекции, и потому рассмотрим законы проецирования на три плоскости проекции.

Пусть заданы три взаимно перпендикулярные плоскости проекций, образующих прямой трехгранный угол (рис.1.5.): П₁ – горизонтальная, П₂ – фронтальная и П₃ – профильная плоскости проекций; линии Оx, Оy, Оz взаимного пересечения плоскостей проекций называются осями проекций, а точка О – началом осей проецирования.

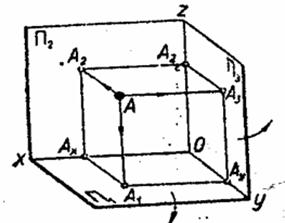
Рис. 1.5.

В пространстве трехгранного угла задана точка А и требуется построить ее проекции на плоскости П₁, П₂, П₃ (точку можно рассматривать как вершину некоторого предмета). Для этого из точки А проводят проецирующие лучи АА₁, АА₂, АА₃, перпендикулярные к плоскостям проекций, до пересечения с ними. В результате пересечения получают А₁ – горизонтальную, А₂ – фронтальную, А₃ – профильную проекции точки А. Прямая АА₁ называется горизонтально проецирующим, АА₂ – фронтально проецирующим, АА₃ – профильно проецирующим лучами. Проецирующие лучи АА₁ и АА₂ определяют плоскость перпендикулярную к оси Ох и ∩ плоскостям П₁, П₂ пересекает плоскости проекций по прямым А₁А_х и А₂А_Х, перпендикулярно к оси Ох. Точку пересечения этой плоскости с осью Ох обозначают А_х. Рассуждая аналогично, получают прямые А₁А_у и А₃А_у, перпендикулярные к оси Оу, и прямые А₂A_z и А₃A_z, перпендикулярные к оси Оz.

1.3 Задание точки на комплексном чертеже Монжа (или эпюр Монжа).

1.3.1 Проецирование точки на две плоскости проекций. Четверти пространства

Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Основные принципы построения таких чертежей изложены Гаспаром Монжем - крупным французским геометром конца 18, начала 19 веков. Изложенный Монжем метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций был и остается основным методом составления технических чертежей.

Две взаимно перпендикулярные плоскости (рис. 1.6) проекций П₁ – горизонтальная плоскость проекций, П₂ – фронтальная плоскость проекций делят пространство на четыре квадранта (четверти):

I квадрант – передний верхний,

II квадрант – задний верхний,

III квадрант – задний нижний,

Дата добавления: 2013-12-13