ЛЕКЦИЯ 1. В) горизонтальная А1 и профильная А3 проекции точки всегда расположены на линиях связи, пересекающихся на биссектрисе угла у1Оу3

В) горизонтальная А1 и профильная А3 проекции точки всегда расположены на линиях связи, пересекающихся на биссектрисе угла у1Оу3. Эта биссектриса получила наименование постоянной прямой чертежа (линия К), а линия связи А1А0А3 – ломаной или горизонтально- вертикальной линии связи.

А2Ах=АА1=ZА – апликата (высота) точки

А1Ах=АА2=УА – ордината (глубина) точки

Прямая линия А2А1, соединяющая две проекции точки на чертеже, называется линией связи.

Плоскости П1 и П2 пересекаются по прямой, называемой осью проекций (осью абсцисс).

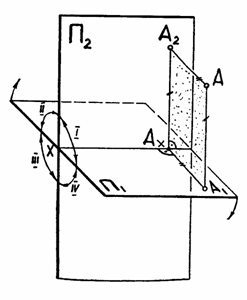
Рис. 1.6

Пусть дана точка А в I квадранте и требуется спроецировать её (ортогонально) на плоскости П₁ и П₂.

Спроецировать ортогонально точку А – значит геометрически опустить из точки А на плоскости проекций П₁ и П₂ перпендикуляры.

АА₂^П₂

АА₁^П₁

Построим комплексный чертеж (эпюр) т. А, т.е. плоский чертеж, состоящий из двух проекций т. А (рис. 1.7). Для этого мысленно удаляют т. А и проецирующие прямые АА₁ и АА₂, а затем вращают плоскость П₁ вокруг оси Х до совмещения с плоскостью П₂, вращая плоскость П₁ так, чтобы передняя полуплоскость П₁ оказалась под осью Х в совмещенном положении (см. стрелки рис. 1.6).

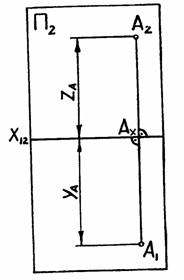
Рис. 1.7.

Отрезок А₁А_х равен расстоянию от точки А до фронтальной плоскости проекций П₂, называемому ординатой точки А или глубиной точки А.

Отрезок А₂А_х равен расстоянию от точки А до горизонтальной плоскости проекций П, называемому аппликатой точки А или высотой точки А.

Прочитать чертеж точки А, значит перегнуть его мысленно по оси Х_х (ось абсцисс), восстановить перпендикуляры из проекций точки А, и тогда точка пересечения их будет точкой А, заданной комплексным чертежом. Таким же образом доказывается и то, что две проекции точки вполне определяют положение точки в пространстве.

Построение чертежей точек по координатам упрощается, если нанести координатные оси аппликат Z и ординат Y на наглядном рисунке плоскостей проекций П₁ и П₂ и на комплексном чертеже точки (рис. 1.8)

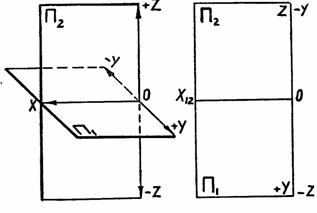
Рис. 1.8.

Таблица 1

В начертательной геометрии принята левая система координат, когда положительная полуось абсцисс Х направлена влево.

Построение эпюра (чертежа) точки по наглядному рисунку точки в пространстве, расположенной в той или иной четверти, проще начинать с построения фронтальной проекции точки, откладывая на эпюре по направлению линии связи размер высоты точки, а после этого надо представить себе и решить, куда – вниз или вверх будет перемещаться горизонтальная проекция точки с той горизонтальной полуплоскостью, на которой она расположена, и только тогда можно решить, где над осью Х-ов, или под осью Х-ов будет расположена горизонтальная проекция точки на эпюре.

Построение наглядного рисунка точки в пространстве, расположенной в том или ином квадранте по заданному эпюру точки, лучше также начинать с фронтальной проекции, откладывая размер А₂А_х высоты точки А. После этого надо решить вопрос, на какой горизонтальной полуплоскости проекции, передней или задней, должна лежать горизонтальная проекция точки. Если на эпюре горизонтальная проекция точки лежит под осью абсцисс, то она на наглядном рисунке будет расположена на передней горизонтальной полуплоскости. Если над осью абсцисс, то – на задней горизонтальной полуплоскости.

1.3.2 Проекции точки на три плоскости проекций. Октанты пространства

В начертательной геометрии принято от пространственного изображения точки и ее проекций переходить к плоскому, или комплексному, чертежу, образованному вращением плоскости проекций вокруг осей проекций (рис. 1.9.).

Сохраняя неподвижной фронтальную плоскость проекций П₂, горизонтальную плоскость П₁ поворачивают вокруг оси Ох вниз на 90^о, а профильную – вокруг оси Оz вправо на 90^о до их совмещения с фронтальной плоскостью проекций. Направление вращения показано на рис. 1.5. стрелками.

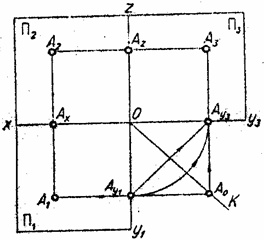
Рис. 1.9.

Полученное изображение трех плоскостей проекций вместе с изображенными на них проекциями А₁, А₂, А₃ точки А называют комплексным чертежом точки А. На комплексном чертеже ось Оу раздваивается и кроме вертикального положения Оу₁ (вниз от точки О) занимает и второе – горизонтальное положение Оу₃ (вправо от точки О).

Прямую, соединяющую две проекции точки на комплексном чертеже, называют линией связи.

Из анализа рис. 1.9 вытекают следующие основные положения:

а) горизонтальная А₁ и фронтальная А₂ проекции точки всегда расположены на вертикальной линии связи, перпендикулярной к оси проекций Ох;

б) Фронтальная А₂ и профильная А₃ проекции точки всегда расположены на горизонтальной линии связи, перпендикулярной к оси проекций О_Z;

В начертательной геометрии часто приходится решать задачи на построение третьей проекции фигуры по двум данным. Для этого прежде нужно научиться строить третью проекцию точки, если известны две ее проекции. Выполнить это можно тремя способами.

Проекционный способ (рис 1.9).Из фронтальной проекции А₂ проводят горизонтальную линию связи. Из горизонтальной проекции А₁ опускают перпендикуляр на ось Оу₁, получают точку Ау₁, и при помощи циркуля или прямоугольного равнобедренного треугольника находят на оси Оу₃ положение точки Ау₃. из этой точки проводят вертикальную линию связи до пересечения с линией связи, проведенной из А₂. Точка А₃ – профильная проекция точки А.

Координатный способ. Из фронтальной проекции А₂ проводят горизонтальную линию связи. Измеряют циркулем расстояние от проекции А₁ до оси Ох (глубину точки, или координату у_А) и откладывают этот отрезок на линии связи вправо от точки А_Z. Получают профильную проекцию А₃.

Способ с использованием постоянной прямой чертежа. Из фронтальной проекции А₂ проводят горизонтальную линию связи. Из горизонтальной проекции А₁ проводят линию связи до пересечения в точке А₀ с постоянной прямой К, т.е. биссектрисой угла у₁Оу₃. из точки А₀ проводят вертикальную линию связи до пересечения с линией, проведенной из фронтальной проекции А₂.

Предпочтительней второй и третий способы, требующие меньшего числа построений и позволяющие использовать чертежные приборы.

Если принять плоскость и оси проекции за координатные плоскости и оси координат х у, z, то положение любой точки пространства может быть задано тремя ее координатами. В этом случае (рис.1.10):

х – широта точки (ее удаление от профильной плоскости проекций) или расстояние от точки А_Х до начала осей проекции О (АА₃ = А_ХО).

у – глубина точки, измеряют ее расстоянием от фронтальной плоскости проекций или удалением ее горизонтальной проекции А₁ от оси Ох (АА₂ = А₁А_х).

Z – высота точки, определяется ее расположением от горизонтальной плоскости проекций или удалением ее фронтальной проекции А₂ от точки Ох (АА₁ = А₂А_х).

Рис. 1.10.

Запись типа А (10, 16, 8) означает, что координата х точки А равна 10мм, координата у=16 мм, координата z= 8 мм.

Наиболее удобной для фиксирования положения геометрической фигуры в пространстве является декартова система координат, состоящая из трех взаимно перпендикулярных плоскостей:

П₁ – горизонтальная плоскость проекций;

П₂ – фронтальная плоскость проекций;

П₃ – профильная плоскость проекций;

Ось х – ось абсцисс;

Ось у – ось ординат;

Ось z – ось аппликат;

О – начало координат.

Положительными направлениями оси считают: для оси х – влево от начала координат, для оси у – в сторону зрителя от плоскости П₂, для оси z – вверх от плоскости П₁, противоположные направления осей считаются отрицательными (рис. 1.11.).

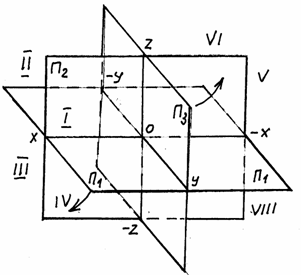
Рис. 1.11.

Плоскости проекции делят пространство на 8 частей – октантов, каждый из которых представляет собой прямоугольный треугольник, где гранями являются части плоскостей проекций, а ребрами – оси координат.

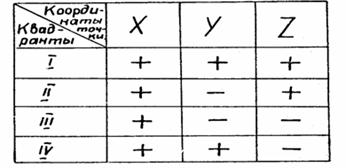
Учитывая при отсчете координат направления осей х, у, z, получим знаки координат для каждого октанта (табл. 2).

Возможны следующие случаи.

Точка расположена в пространстве. В этом случае ее зададут тремя координатами (измерениями). Все три проекции точки удалены от осей проекций (рис.1.9).

Точка находится на одной из плоскостей проекций – П₁, П₂ или П₃. В этом случае ее задают двумя действующими координатами, не равными нулю. Одна проекция совпадает с самой точкой, а две другие лежат на осях. На рисунке 1.12 изображены проекции точки В (20, 0, 15), лежащей в плоскости проекций П₂. В этом случае фронтальная проекция В₂ совпадает с самой точкой В, горизонтальная проекция В₁ лежит на оси Ох, а профильная В₃ – на оси Оz.

Точка находится на одной из осей проекций – Ох, Оу, Оz. В этом случае ее задают одной действительной координатой, не равной нулю. Две проекции совпадают с самой точкой, а третья находится в точке О – начале осей проекций. На рисунке 1.10 изображены проекции точки С (15, 0, 0), лежащей на оси Ох. В этом случае горизонтальная С₁ и фронтальная С₂ проекции совпадают с самой точкой С, а профильная проекция С₃ находится в точке О.

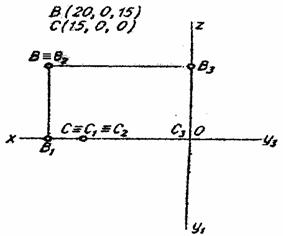
Рис.1.12

1.4 Обратимость чертежа

Проецированием на одну плоскость проекций получается изображение, которое не позволяет однозначно определить форму и размеры изображенного предмета. Проекция А₁ (см. рис. 1.4.) не определяет положение самой точки в пространстве, так как неизвестно, на какое расстояние она удалена от плоскости проекций П₁. В таких случаях говорят о необратимости чертежа, так как по такому чертежу невозможно воспроизвести оригинал. Для исключения неопределенности изображения дополняют необходимыми данными. В практике применяют различные способы дополнения однопроекционного чертежа.

Дата добавления: 2013-12-13