Кривизна плоской кривой

План лекции

2.1. Кривизна плоской кривой

2.2. Уравнения кривой в пространстве. Вектор-функция скалярного аргумента

Первая производная f¢(x) функции f(x) дает простую характерис­тику кривой y = f(x) – ее направление. Вторая производная f²(x) связана с другой характеристикой кривой, кривизной, или искривленностью кривой.

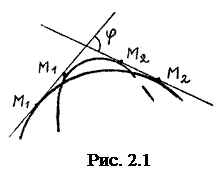
Предположим, что кривая не пере­секает себя и в каждой точке имеет касательную. Выберем две точки на кривой M₁ и М₂, проведем касатель­ные к кривой в точках M₁, М₂ и угол между касательными обозначим j (рис. 2.1). Этот угол называется углом смежности дуги кривой M₁М₂. Угол смежности в некоторой степени дает представление об изогнутости дуги M₁М₂, так как j является тем углом, на который поворачивается касательная при перемещении

точки касания от начальной точки дуги M₁ до конечной М₂, чем больше угол смежности j, тем, очевидно, больше изогнутость дуги. Но один и тот же угол смежности могут иметь две дуги с явно различной изогнутостью. Поэтому для характе­ристики изогнутости угол смежности дуги рассчитывается на единицу ее длины.

Определение. Отношение угла смежности дуги к ее дли­не называется средней кривизной дуги: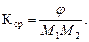

Чем меньше дуга M₁М₂, тем лучше средняя кривизна характеризует изогнутость линии вблизи точки M₁.

Определение. Кривизной К линии в точке M₁ называется предел средней кривизны К_ср дуги M₁М₂ при стремлении конеч­ной точки дуги М₂ к ее начальной точке M₁ (рис. 2.2):

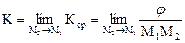
В частности, для окружности радиуса r: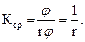

Средняя кривизна окружности – величина постоянная, значит, кривизна – тоже постоянна. У прямой на плоскости кривизна также постоянна и равна 0. У всех других линий кривизна меняется от точки к точке.

Если кривая задана уравнением y = f(x), то кривизну можно вычис­лить по формуле (вывод формулы опускаем):

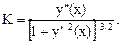
Если кривая задана в параметриче­ском виде x = j(t), у = y(t), то

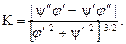
Определение. Величи­на R, обратная кривизне K линии в данной т. М, называется радиусом кривизны этой линии в т. М: R =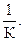

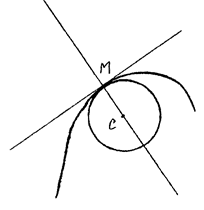
Если провести нормаль в т. M и отложить на ней в сторону вогнуто­сти кривой отрезок, равный R, то получим точку С, которая называется центром кривизны кривой в точке М, а круг радиуса R с центром в точке С – кругом кривизны данной кри­вой в точке М (рис. 11.3).

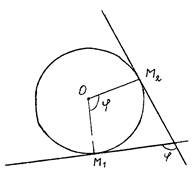Рис. 2.2 Рис. 2.3

Координаты центра кривизны находятся по формулам: С (X, У),

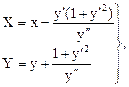(2.1)

если кривая задана уравнением y = f(x), а точка M имеет координаты x, y.

Если кривая задана в параметрическом виде, то координаты центра кривизны в т. С (Х, У):

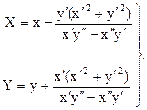(2.2)

Ясно, что каждой точке М на кри­вой соответствует определенный центр кривизны; совокупность всех центров кривизны данной кривой образует линию, которую называют эволютой данной кривой, а данную кривую, по отношению к эволюте, называют эвольвентой.

Из определения эволюты следует, что формулы (2.1), (2.2) являются параметрическими уравнениями эволюты (в первом случае параметром является x, во втором – t).

Пример 1. Найти радиус кривизны кривой xy = 4 в точке (2, 2).

Решение: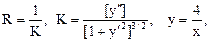

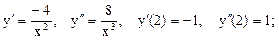
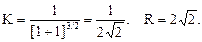
Пример 2. Найти уравнение эволюты эллипса x = acos t, y = bsin t и построить эллипс и его эволюту.

Решение: уравнения эволюты ищем в виде (2.2). Для этого нужно найти x¢, x², y¢, y²:

x¢ = –asin t, x² = –acos t, y¢ = bcos t, y² = –bsin t;

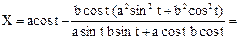
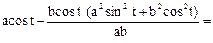
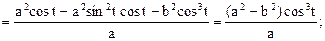
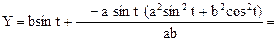
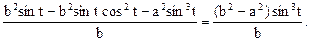
Уравнения эволюты эллипса в параметрической форме:

,

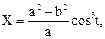
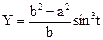или, так как для эллипса a² – b² = c², то

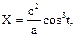
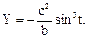
Построим эллипс и его эволюту (рис. 2.4).

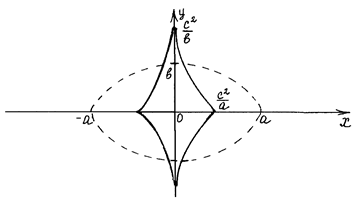Рис. 2.4

2.2. Уравнения кривой в пространстве.

Вектор-функция скалярного аргумента

Линия в пространстве – это геометрическое место точек пересече­ния двух поверхностей:

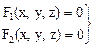– уравнения кривой в общем виде.

Рассмотрим кривую в пространстве и произвольную ее точку A(x, y, z) (рис. 2.5). Вектор 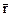, проведенный из начала координат в точку А, можно представить:

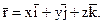
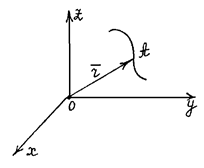Рис. 2.5

Предположим, что

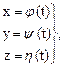(2.3)

тогда

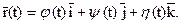(2.4)

Уравнения (2.3) называют параметрическими уравнениями линии в пространстве, а уравнение (2.4) – векторным уравнением линии.

Пример 3. Пусть дана прямая каноническими уравнениями:

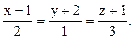
Введя параметр t, получим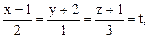

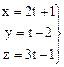– параметрические уравнения той же прямой, а

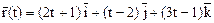– векторное уравнение прямой.

Функцию (11.3) называют вектор-функцией скалярного аргумента t.

Если при t ® t_о, j(t) ® j (t_о), y(t) ® y(t_о), h(t) ® h (t_о),

то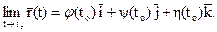

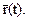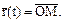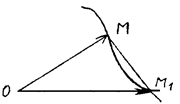
Найдем производную функции Параметру t соответствует Дадим t приращение ∆t, получим значение параметра t + ∆t, ему соответствует 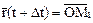(рис. 2.6).

Рис. 2.6

Тогда ,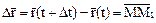

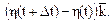
Вычислим предел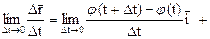

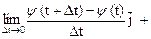
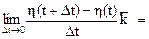
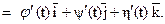
Этот предел называется производной вектор-функции скалярного аргумента в точке М и обозначается: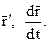

Отметим, что если ∆t ® 0, то т. М₁ ® М и секущая ММ₁ занимает предельное положение, т.е. вектор 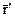направлен по касательной к кривой в точке М. Ясно, что производная функции 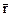существует при выбранном значении параметра t, если существуют j¢(t), y¢(t), h¢(t).

Дата добавления: 2013-12-13