Цифровой ЛКГ-регулятор (Цифровое линейно-квадратичное гауссовское управление)

В ЛКГ задаче предполагается, что объект управления удовлетворяет уравнениям (11a) и (11b), а критерий качества определяется как математическое ожидание выражения (2а)

. (18)

Задача заключается в том, чтобы найти управление u [ i ], которое минимизирует (18) при ограничениях (11a) и (11b). Показано, что и в данном случае справедлива теорема разделения, согласно которой оптимальный закон управления является обратной связью по состоянию

,

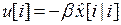и задачу проектирования можно разделить на две части и решить каждую из них в отдельности. Первая задача ̶ это задача цифрового ЛК управления, рассмотренная в параграфе 3.29 и решение которой дает 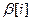, а вторая ̶ задача оценивания состояния 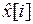с помощью фильтра Калмана (оптимального наблюдателя состояния), рассмотренная в предыдущем параграфе. Замкнутая система ЛКГ управления описывается следующими уравнениями

,

,

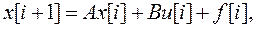
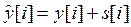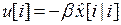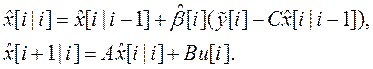
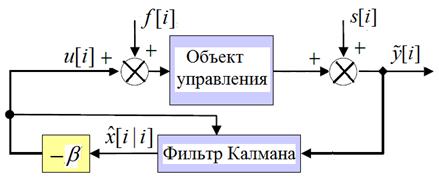
Структурная схема ЛКГ управления показана на рис. ниже.

Приведем некоторые дополнительные ограничения, касающиеся рассмотренных задач оптимизации:

- Весовая матрица состояния Q должна быть положительной полуопределенной (),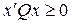

- Весовая матрица управления R должна быть положительной определенной (),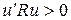

- Объект управления должен быть стабилизируемым, (все неустойчивые моды являются управляемыми), другими словами, пара матриц A и B должна быть обнаруживаемой,

- Объект управления должен быть обнаруживаемым (все неустойчивые моды являются наблюдаемыми), другими словами, пара матриц A и C должна быть обнаруживаемой.

Робастность оптимальных ЛК и ЛКГ систем.

Достоинство ЛК регулятора состоит в том, что он обеспечивает устойчивость замкнутой системы при произвольно выбранных весовых матрицах Q и R. Если матрица R выбрана диагональной, то замкнутая система будет иметь бесконечно большой запас устойчивости по амплитуде и превышающий 60 градусов запас устойчивости по фазе по каждому скалярному входу объекта управления, что говорит о большой робастности и большой относительной устойчивости такой системы. Кроме того, фильтр Калмана обладает такими же робастными свойствами.

Однако ЛКГ система управления может иметь произвольно малыми запасами устойчивости. При этом увеличение быстродействия наблюдателя может повлечь за собой уменьшение запасов устойчивости.

Дата добавления: 2014-01-04