Модели нелинейных систем управления

Нелинейными системами автоматического управления будем называть системы, которые содержат хотя бы один нелинейный элемент. Различают статические нелинейные элементы, математические модели которых можно представить в виде нелинейных статических характеристик (нелинейных алгебраических уравнений), и динамические, процессы в которых описывают нелинейные дифференциальные уравнения.

Основной математической моделью нелинейных звеньев и систем является нелинейное обыкновенное дифференциальное уравнение. В общем случае поведение многомерных систем описывают следующие уравнения состояния и выхода:

(1)

где х. - n- мерный вектор состояния; u - r -мерный вектор управления, 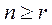; у - l -мерный вектор выходных переменных; f(t,x,u) и g(t,x) - нелинейные вектор - функции. Зависимость этих функций от t отражает действие возмущений. Причем под возмущением понимают как влияние окружающей среды (сигнальное возмущение), так и изменение параметров самого объекта (параметрическое возмущение).

В частном случае управляющее воздействие может входить в уравнение состояния (1) в виде суммы с нелинейными коэффициентами

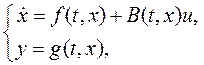(2)

где B(t,x) - матрица нелинейных коэффициентов размера .

Систему, поведение которой описывают уравнения (2), будем называть нелинейной нестационарной системой с афинным управлением.

Если параметры системы с течением временем не меняются, а возмущающие воздействия пренебрежимо малы, то она называется нелинейной стационарной системой. Ее модель имеет вид

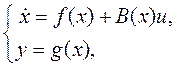(3)

В случае, когда отсутствует управляющее воздействие в (2), система называется нелинейной нестационарной автономной и описывается уравнениями

(4)

Если правая часть уравнений (4) не зависит от времени t, то мы будем говорить о нелинейной стационарной автономной системе.

Примеры нелинейных объектов управления.

Пример 1. Маятник.

Рассмотрим маятник на рис. выше, динамика которого описывается нелинейным уравнением

,

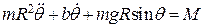где R -длина маятника, m - его масса, b - коэффициент вязкого трения в шарнире, g - ускорение силы тяжести, M –приложенный к маятнику момент. Обозначая 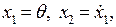запишем уравнение маятника в переменных состояния

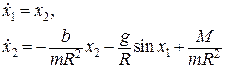
или

,

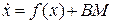где

Пример 2. Два соединенных резервуара.

В качестве объекта управления рассмотрим два соединенных резервуара, в которых фактически можно измерить только уровень жидкости во втором резервуаре. Однако также нас интересует и оценка уровня жидкости в первом резервуаре. Схематическое изображение ОУ представлено на рис. ниже.

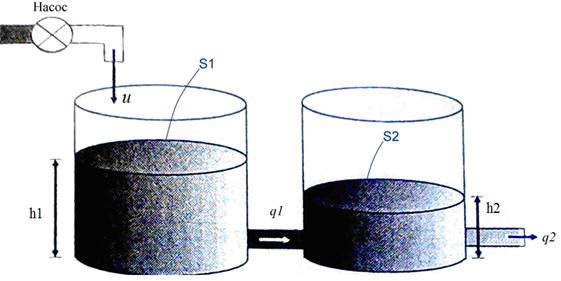
Вода течет в первый резервуар через насос со скоростью u, что влияет на уровень воды в резервуаре 1 (обозначенный через h1). Вода вытекает из резервуара 1 в резервуар 2 со скоростью q1, воздействуя на уровни h1 и h2. Наконец, вода вытекает из резервуара 2 со скоростью q2.

Для данного процесса получены дифференциальные уравнения, которые связывают скорости потоков и уровни:

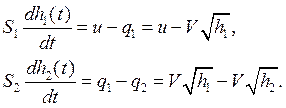
или

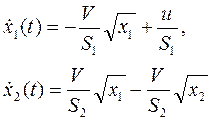, (9)

где площадь поперечного сечения баков 1 и 2 соответственно; 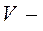объемная составляющая баков.

Полагая 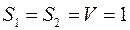, 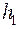= , 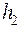= 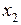, получаем следующие выражения:

где 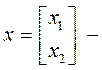вектор состояния.

После подстановки всех данных в формулу (1), уравнения объекта управления принимают вид:

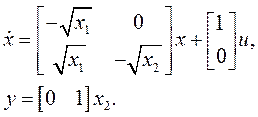
Как видим, порядок объекта управления равен 2, т.е. n=2.

Пример 3.

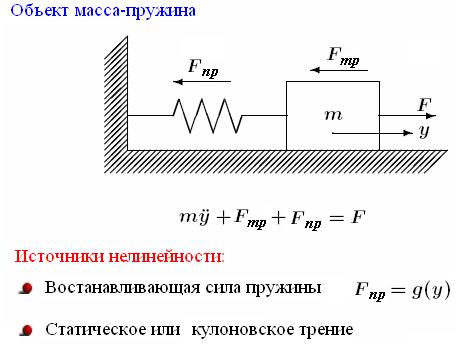
где h - коэффициент вязкого трения.

Вводя переменные состояния и пренебрегая статическим трением, запишем уравнения объекта масса-пружина-трение в переменных состояния

Если вязкое трение описывается нелинейным уравнением, то вместо 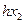имеем, например, .

Дата добавления: 2014-01-04