Способ Гольдфарба

Решение основного уравнения метода гармонического баланса (17) относительно амплитуды и частоты автоколебаний можно получить графически.

В способе Гольдфарба, прежде всего, предлагается разрешить основное уравнение относительно частотной характеристики линейной части системы:

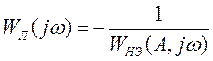. (18)

Затем на комплексной плоскости строятся амплитудно-фазовая характеристика 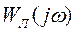и характеристика, соответствующая нелинейному элементу, т. е. обратная частотная характеристика нелинейного элемента,

. (19)

Если эти две характеристики не пересекаются, то периодических процессов в нелинейной системе не возникает.

При наличии пересечений частота автоколебаний определяется по частотной характеристике линейной части системы 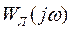, а амплитуда - по характеристике нелинейного элемента в точке пересечения.

Поскольку в общем случае точек пересечения и характеристики нелинейного элемента (19) может быть несколько, в системе могут возникать соответствующие им периодические процессы различных амплитуды и частоты. Причем часть из них будут устойчивыми, а часть - неустойчивыми.

Устойчивость найденного колебательного режима позволяет оценить следующее правило (оно не является строго обоснованным, но зачастую оказывается достаточным). Если при движении по обратной частотной характеристике нелинейного элемента в сторону увеличения амплитуды происходит пересечение амплитудно-фазовой характеристики линейной части «изнутри наружу», то этой точке пересечения соответствуют устойчивые колебания (автоколебания). В противном случае колебания будут неустойчивыми.

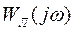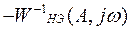На рис. 8 характеристики и пересекаются в двух точках. Это означает, что в системе могут возникать два вида колебаний.

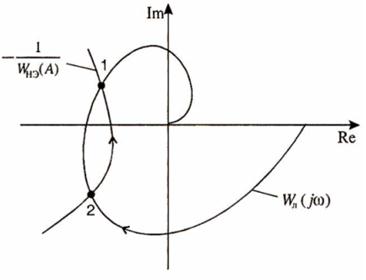
Рис. 8

Причем первой точке пересечения соответствуют устойчивые колебания (автоколебания) с амплитудой A ₁ и частотой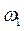, а второй точке - неустойчивые.

Пример.

Определить параметры колебаний и проверить их устойчивость для системы, изображенной на рис. 6. Здесь нелинейный элемент представляет собой идеальное реле (см. рис. 5) с уровнем ограничения 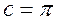, а передаточная функция линейной части следующая:

.

Получим выражение для амплитудно-фазовой характеристики (рис. 9) в виде

,

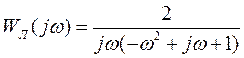или

.

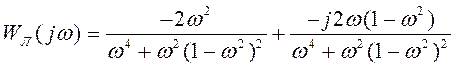Запишем выражение для частотной характеристики нелинейного элемента, а затем построим годограф (рис. 9)

.

Как видим, эти характеристики пересекаются в одной точке, которая соответствует автоколебаниям. Для определения их параметров найдем координаты точки пересечения, для чего приравняем нулю мнимую часть 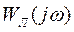: Рис. 9

.

Отсюда следует, что .

При найденном значении частоты получим

.

Из условия

,

определим амплитуду автоколебаний: .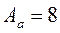

Дата добавления: 2014-01-04