Нахождение максимального потока: алгоритм и теорема

Пусть некоторый поток в сети же имеется, например, поток с нулевыми значениями на всех дугах. Алгоритм Форда – Фалкерсона состоит из двух чередующихся процедур – помечивания вершин и изменения потока. Помечивание вершин. Вершины снабжаются метками, состоящими из двух элементов. Источник получает условную метку 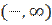. Теперь пусть имеется некоторое множество помеченных вершин. выбираем любую из них и обрабатываем ее. Обработка -ой вершины с меткой 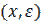состоит в помечивании из вершины смежных непомеченных вершин по следующему правилу: если , то вершине присваивается метка ; если , то вершине присваивается метка . Затем обрабатывается другая помеченная вершина и так далее. Процесс помечивания заканчивается в двух случаях: 1) Ни одну вершину больше нельзя пометить, но сток не помечен. Тогда алгоритм останавливается. 2) Сток помечен. Тогда производится изменение потока.

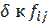Изменение потока. Пусть сток получил метку . Тогда прибавляем и переходим в вершину . Общий шаг: если мы находимся в вершине с меткой , то прибавляем к и переходим в 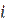. А если метка равна 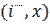, то вычитаем и переходим в 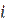. Заметим, что правило формирования меток таково, что после прибавления 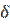новое значение потока не превышает пропускной способности дуги, а при вычитании не получается отрицательной величины. Продолжаем изменение потока, пока не достигнем источника. Почему это непременно случится? Представим себе, что мы нумеруем вершины по мере их помечивания. Тогда вершины, помеченные из 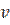, получают номер, больший, чем номер вершины 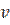. При изменении потока переход совершается наоборот, от вершины с большим номером к вершине с меньшим номером. Пока не достигнем вершины номер один – источника. Следует еще убедиться в том, что при изменении потока не нарушается условие 2) в определении потока. При прохождении вершины возможны четыре случая:

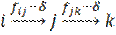, , , . Условие 2) выполняется во всех случаях.

Величина измененного потока на 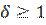больше, чем у исходного потока. Теперь снова переходим к помечиванию. Схема алгоритма такова:

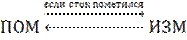
Поскольку поток увеличивается не меньше, чем на единицу, а величина потока не может превышать пропускной способности любого разреза, то алгоритм останавливается после конечного числа шагов.

Теорема 1. Поток , вычисленный алгоритмом, имеет максимальную величину, а разрез , где - множество вершин, помеченных при последнем помечивании, имеет минимальную пропускную способность.

Доказательство: Для всякой дуги , где , верно . Действительно, если допустить, что , то должна быть помечена из 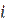по первому правилу помечивания. А для всякой дуги , где 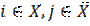, верно , поскольку при вершина должна была быть помечена из 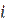по второму правилу помечивания. В силу этих свойств , и утверждение теоремы следует из леммы 3.

Теорема 2 (о максимальном потоке и минимальном разрезе). В любой сети существует максимальный поток. Величина максимального потока равна пропускной способности минимального разреза.

Рассмотреть пример.

Предложение 1. Если в сети существует -путь, то с ней имеется поток положительной величины. Обратно, если в сети задан поток положительной величины, то существует -путь, на дугах которого поток положителен.

Дата добавления: 2014-01-04