Гармоническое векторное поле

Векторное поле , являющееся одновременно и потенциальным, и соленоидальным, называется гармоническим векторным полем.

Отметим следующие свойства гармонического векторного поля.

1). Гармоническое векторное поле обладает скалярным и векторным потенциалом.

2). Скалярный потенциал 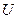является функцией гармонической.

3). Для гармонического векторного поля 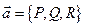его координаты 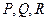являются функциями гармоническими.

Проверим эти свойства.

1). Первое свойство следует из определения, т.к. потенциальное поле обладает скалярным потенциалом, а соленоидальное поле обладает векторным потенциалом.

2). Так как гармоническое поле потенциально, то оно обладает скалярным потенциалом 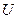и представимо в виде 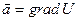. С другой стороны, гармоническое поле является соленоидальным, поэтому

.

Таким образом, потенциал 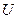гармонического поля удовлетворяет уравнению Лапласа и является гармонической функцией.

3). Для гармонического векторного поля 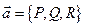в силу его потенциальности 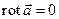, т.е. или

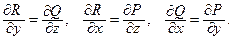(12.5)

В силу соленоидальности гармонического векторного поля 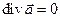, т.е. 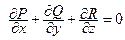. Продифференцируем это равенство по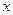

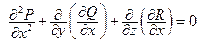
и воспользуемся вторым и третьим из равенств (12.5):

или .

Это значит, что функция 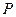является гармонической. Аналогично можно показать, что функции 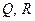являются гармоническими.

Дата добавления: 2014-01-04