ЛЕКЦИЯ 19. Понятие об устойчивости сооружений. Устойчивость центрально сжатого стержня в пределах пропорциональности. Формула Эйлера

Надёжность конструкции обеспечивается выполнением условий прочности и жёсткости. Однако эти условия могут быть в некоторых случаях необходимыми, но недостаточными, требуется обеспечить выполнение устойчивости всего сооружения в целом и его отдельных элементов.

Исследованию задач устойчивости сооружений посвящён целый раздел механики деформируемого твёрдого тела – теория устойчивости. В курсе сопротивления материалов рассматривается одна из простейших задач – устойчивость центрально сжатого стержня.

Тела или системы тел могут находиться в состоянии устойчивого, безразличного или неустойчивого равновесия в зависимости от их геометрии, характера внешнего воздействия и др. причин (рис. 19.1).

а) б) в)

Рис. 19.1. Случаи равновесия: а) устойчивое;

б) безразличное; в) неустойчивое

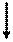
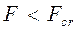
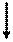
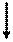а) б) в)

Рис. 19.2. Формы равновесия идеального прямого стержня: а) прямолинейная (устойчивая); б) раздвоение форм равновесия или бифуркация (безразличная форма равновесия); в) потеря прямолинейной формы устойчивости

При решении задач устойчивости может быть использован динамический метод, основанный на исследовании колебаний упругой системы относительно исходного положения равновесия. При этом стержню задают небольшое возмущение (рис. 19.2). Наименьшее значение нагрузки, при которой первоначальная форма равновесия становится неустойчивой, называется критической силой.

В условиях эксплуатации сооружения потеря устойчивости недопустима, поэтому должно выполняться условие устойчивости. Случаи, рассмотренные на рис. 19.2 распространяются на идеализированные стержни, а на практике стержни всегда имеют некоторое искривление оси, связанное с дефектами изготовления или монтажа. Внешние силы действуют не точно по оси стержня, что приводит к возникновению изгибающих моментов, такое состояние называют продольным изгибом. Реальный сжатый стержень находится в равновесном изогнутом состоянии. При расчёте на устойчивость безопасность обеспечивается введением коэффициента запаса устойчивости.

Формула Эйлера для критической силы. Определим критическую силу для центрально сжатого стержня, шарнирно опёртого по концам (рис. 19.3). При F = F_cr кроме продольной силы возникает изгибающий момент.

(19.1)

Предположив, что материал работает линейно, т.е. напряжения в поперечных сечениях не превышают предела пропорциональности и прогибы малы, воспользуемся приближённым дифференциальным уравнением изогнутой оси стержня. Рис. 19.3.

(19.2)

Пусть (19.3)

тогда получим (19.4)

Общее решение этого уравнения имеет вид

(19.5)

Здесь три неизвестных: С₁, С₂, k. Запишем граничные условия: v(0) = 0, v(l) = 0. Из первого С₂ = 0, а из второго получим

(19.6)

Из (19.5) следует, что либо С₁ = 0 (в этом случае прогибы во всех сечениях 0, но это противоречит принятым предположениям), либо sinkl = 0. Последнее выполнится в случае kl = n π, где n – целое число. С учётом этого по формулам (19.3) и (19.5) получим

(19.7)

(19.8)

Это задача на собственные значения, найденные числа k = n π / l называются собственными числами, а функции собственными функциями. Согласно (19.8) стержень изгибается по n полуволнам синусоиды (рис. 19.4). Наименьшее значение силы будет при n = 1

(19.9)

Эта формула получена Леонардом Эйлером и называется формулой Эйлера для критической силы. При этом kl = π, а изогнутая ось стержня представляет собой одну полуволну синусоиды (рис. 19.4а)

(19.10)

здесь - прогиб в середине стержня.

а) б) в)

Рис. 19.4

Все формы равновесия (рис. 19.4), кроме n = 1, неустойчивы и не представляют практического интереса, но их можно превратить в устойчивые введением дополнительных опор.

Полученное решение обладает двумя особенностями. Во-первых, решение (19.10) не является единственным, т.к. осталась неопределённой. В результате прогибы оказались определены с точностью до постоянного множителя. Во-вторых, это решение не даёт возможности описать состояние стержня при F > F_cr.

Влияние способов закрепления стержня на величину критической силы. Формула Эйлера получена для стержня шарнирно опёртого по концам. Аналогично можно получить выражения для критической силы и при других условиях закрепления стержня.

(19.11)

где величина

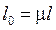(19.12)

называется приведённой длиной стержня, а μ – коэффициентом приведения длины.

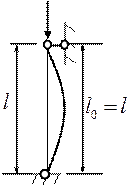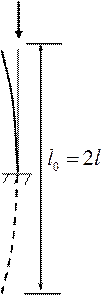Рис. 19.5.

Величина l₀ – расстояние между точками перегиба, где изгибающий момент равен нулю. Поделив критическую силу на площадь поперечного сечения, получают критическое напряжение.

(19.13)

Учитывая, что I / A = i ² введём обозначение

(19.14)

В этом случае критическое напряжение можно записать как

(19.15)

Величину λ называют гибкостью стержня.

Дата добавления: 2014-01-04