Вывод формул численного дифференцирования

ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ

Лекция 20.

Источником формул численного дифференцирования является полиномиальная интерполяция.

Зная в точках x_i:=x_i+ih (i = 0,1,..., п) при некотором h > 0 значения y_i:=f (x_i) данной функции f (x), можно найти конечные разности D ^ky_i и записать для нее, например, первый интерполяционный многочлен Ньютона Р_п (х) (см. § 17.1). Дифференцируя приближенное равенство f (x)» Р_п (х), будем строить формулы приближенного дифференцирования разной точности в зависимости от степени п используемого интерполяционного многочлена. Через вспомогательную переменную 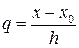приближенное представление функции f (x) по первой формуле Ньютона выглядит наиболее просто (см. (17.3):

(20.1)

Отсюда получаем конечноразностную формулу численного дифференцирования

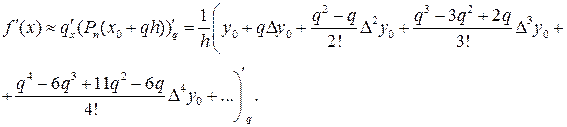
т.е.

(20.2)

При использовании последнего равенства для приближенного вычисления производной функции f (x) в заданной точке 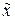из некоторой окрестности точки х ₀ следует найти соответствующее значение переменной 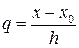и подставить его в формулу (20.2). Максимальный порядок конечных разностей в этой формуле при желании получить производную с наибольшей точностью определяется в конкретной ситуации в соответствии с приведенными в §§ 17.1, 17.2 соображениями о выборе подходящей степени интерполяционного многочлена.

Рассмотрим несколько частных случаев формулы (20.2), фиксируя степень п лежащего в ее основе интерполяционного многочлена (20.1) равной 1, 2, 3. Этим значениям п отвечают соответственно одно, два, три первых слагаемых в формуле (20.2). Таким образом, имеем:

на основе линейной интерполяции

(20.3)

на основе квадратичной интерполяции

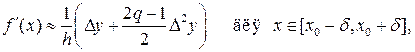(20.4)

на основе кубической интерполяции

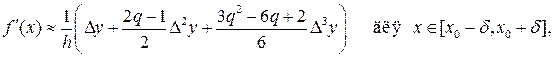(20.5)

и т.д. (при некоторых d > 0, определяющих промежуток экстраполяции приемлемого качества соответствующей интерполяционной формулой).

Для дальнейшего особый интерес представляют частные случаи формул (20.3)-(20.5), связывающие приближенное значение производной функции f (x) в узлах х ₀, х ₁,... с узловыми значениями самой функции. Учитывая, что точкам х ₀, х ₁, х ₂, х ₃,

соответствуют значения q = 0, 1, 2, 3, и раскрывая конечные разности через значения y_i (i = 0, 1, 2, 3), имеем:

при п = 1 из (20.3)

(20.6)

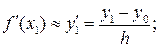(20.7)

при п = 2 из (20.4)

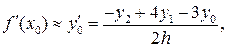(20.8)

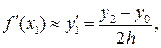(20.9)

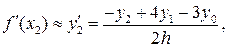(20.10)

при и = 3 из (20.5)

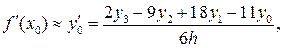
В случае необходимости этот ряд формул можно продолжить с помощью общей формулы (20.2) или посмотреть в учебниках.

Повторное дифференцирование приближенного равенства (20.2), т.е. взятие производной по x от правой части формулы (20.2) с учетом приводит к конечноразностной формуле вычисления второй производной

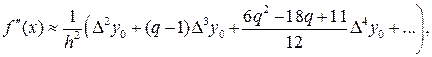(20.11)

из которой таким же образом следует приближенная формула для третьей производной

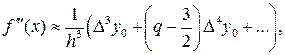
Наиболее важной в приложениях является простейшая аппроксимация второй производной с помощью первого слагаемого, получающаяся из (20.11). В частности, в точке x ₁ имеем приближенное равенство

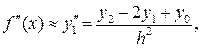(20.12)

которое вместе с формулами (20.6) – (20.10) широко используется при построении конечноразностных методов решения обыкновенных дифференциальных уравнений второго порядка.

Дата добавления: 2014-01-04