Оператор Гамильтона

Трихинеллез.

Методичка.

Рассмотрим символический оператор Гамильтона (или вектор “набла”)

.

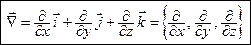С его помощью удобно записать основные операции теории поля:

1) градиент скалярного поля есть произведение вектора на скалярную функцию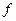

;

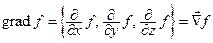2) дивергенция векторного поля есть скалярное произведение вектора на вектор поля

;

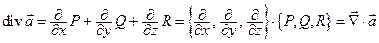3) ротор векторного поля 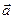есть векторное произведение вектора на вектор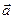

;

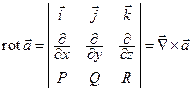4) оператор Лапласа 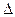скалярного поля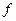

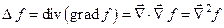или символически ;

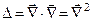5) производная по направлению

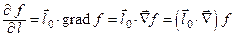или символически .

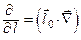Такая запись основных операций поля наиболее часто используется в физических и технических приложениях, связанных с изучением реальных физических полей.

При применении оператора следует учитывать и его векторную и его дифференциальную природу. На этом основаны правила применения . Эти правила можно было заметить при изучении дифференциальных свойств дивергенции, градиента, ротора.

Применение к выражениям, не содержащим произведения переменных

Применение к выражениям, не содержащим произведения переменных, происходит по правилам векторной алгебры. При этом величина, на которую действует оператор 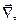должна стоять за ним.

Поясним это правило на следующих примерах.

1). Пусть 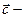постоянный вектор; тогда 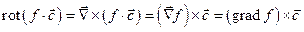; здесь переменная величина 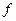перенесена к вектору и поставлена за ним по правилам векторной алгебры (по свойствам векторного произведения скаляр 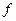можно перенести от второго вектора к первому).

2). Применяя 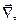получим формулу (13.4):

;

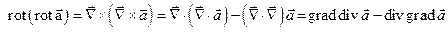здесь мы воспользовались известной формулой для двойного векторного произведения 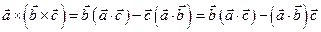; как уже отмечалось, 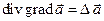для вектора 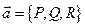понимают как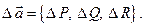

3). Следует иметь в виду, что 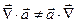, так как 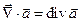есть функция в то время как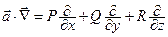есть дифференциальный оператор.

Аналогично, .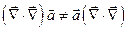

4). Следует иметь в виду, что не является обычным вектором; например,

а) не имеет ни длины, ни направления,

б) 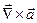не перпендикулярен ,

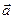в) векторы 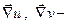не коллинеарны, так как вектор направлен по

нормали к поверхности уровня 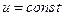, вектор 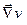направлен по нормали к поверхности уровня .

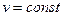Эти примеры показывают, что с вектором следует обращаться с осторожностью и при отсутствии уверенности в полученном результате его следует проверить непосредственно, без использования .

Применение к выражениям, содержащим произведение переменных

В этом случае на первый план выходят дифференциальные свойства оператора и правило дифференцирования произведения.

Результатом действия на произведение переменных является сумма произведений; в каждом из них действует на один множитель, который отмечают штрихом и располагают справа от , соблюдая правила векторной алгебры.

Поясним это правило на следующих примерах.

1). Пусть 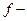функция, 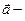переменный вектор; тогда

.

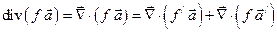Чтобы поставить множитель, помеченный штрихом, рядом с и за ним, воспользуемся двумя свойствами скалярного произведения: скаляр можно переносить от второго вектора к первому и скаляр можно выносить за знак скалярного произведения. Поэтому

.

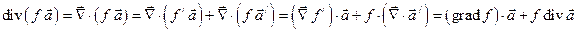2). Пусть 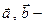переменные векторные поля; тогда

.

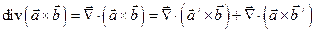Чтобы поставить множитель, помеченный штрихом, рядом с и за ним, воспользуемся свойством векторного произведения 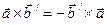и свойством смешанного произведения 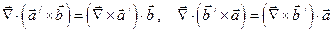. Поэтому

.

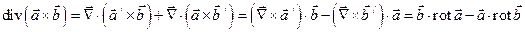Дата добавления: 2014-01-04