Некоторые применения степенных рядов

Числовые и функциональные ряды находят широкое применение в приближенных вычислениях. Остановимся на некоторых из них.

1)Приближенное вычисление значений функций.

Пусть требуется вычислить значения функции 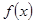в точке с некоторой заданной точностью. Предположим, что функцию можно разложить в степенной ряд

=

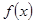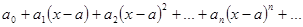
в интервале и что точка 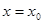принадлежит интервалу.

Тогда, полагая 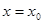, получим числовой ряд

=

Ограничиваясь первыми членами этого ряда, т.е. -ой частичной суммой ряда, получим приближенное равенство

=

Абсолютная погрешность такого приближения равна модулю остаточного члена этого числового ряда:

,

Пример 7 Вычислить число с точностью

Решение:

,

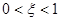
Оценим остаточный член

Если , то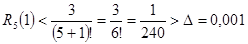

Если , то

Поэтому для достижения заданной точности достаточно положить .

Итак,

.

2)Вычисление пределов функции.

Применение степенных рядов дает весьма эффективный способ раскрытия неопределенности вида , порождаемой разностью 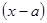, который заключается в том, что числитель и знаменатель дроби раскладываются в степенные ряды по степеням разности 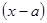, а затем производятся необходимые операции, в результате чего неопределенность обычно исчезает.

Пример 8 Вычислить

Решение:

==.

3)Вычисление производных.

С помощью рядов Тейлора можно находить численные значения производных любого порядка от заданной функции 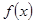. Так, чтобы вычислить производную , нужно разложить функцию 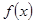в ряд Тейлора по степеням 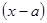, а затем по формуле

= ,

которая получается из общего выражения для коэффициентов ряда, находится производная нужного порядка.

Пример 9 Вычислить для = .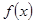

Решение:

Разложим 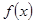в ряд Маклорена

=== =

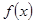, а , то

= .

4)Приближенное вычисление интегралов.

С помощью степенных рядов удается приближенно вычислить ряд интегралов, не выражающихся через элементарные функции, либо вычисление которых другими способами представляет значительные трудности.

Метод основан на том, что если функцию 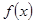можно разложить в равномерно сходящийся на ряд, то этот ряд можно проинтегрировать по любому отрезку 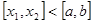, в результате чего определенный интеграл представляется в виде сходящегося ряда. Неопределенные интегралы также можно найти с помощью разложения надинтегральной функции в равномерно сходящийся степенной ряд с последующим интегрированием по отрезку .

Пример 10 Вычислить с точностью .

Решение:

Разложим надинтегральную функцию в степенной ряд, положив .

=

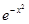Этот ряд сходится на всей числовой оси, 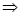, его можно интегрировать по любому отрезку:

= = =

= =

= .

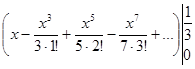Дата добавления: 2014-01-04