
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Функции нескольких переменных
|
|
|
|
Определение. Переменная z (с областью изменения Z) называется функцией двух независимых переменных х,у в множестве М, если каждой паре (х,у) из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z.
Определение. Множество М, в котором заданы переменные х,у, называется областью определения функции, множество Z – областью значений функции, а сами х,у – ее аргументами.
Обозначения: z = f(x,y), z = z(x,y).
Примеры.
- z = xy, z = x ² + y ² - функции, определенные для любых действительных значений х,у.
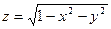 - функция, областью определения которой являются решения неравенства
- функция, областью определения которой являются решения неравенства 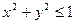 .
.
Определение. Переменная z (с областью изменения Z) называется функцией нескольких независимых переменных  в множестве М, если каждому набору чисел
в множестве М, если каждому набору чисел 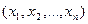 из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятия аргументов, области определения и области значения вводятся так же, как для функции двух переменных.
из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятия аргументов, области определения и области значения вводятся так же, как для функции двух переменных.
Обозначения: z = f 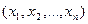 , z = z
, z = z 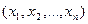 .
.
Замечание. Так как пару чисел (х,у) можно считать координатами некоторой точки на плоскости, то будем впоследствии использовать термин «точка» для пары аргументов функции двух переменных, а также для упорядоченного набора чисел 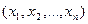 , являющихся аргументами функции нескольких переменных.
, являющихся аргументами функции нескольких переменных.
Геометрическое изображение функции двух переменных
Рассмотрим функцию
z = f(x,y), (15.1)
определенную в некоторой области М на плоскости О ху. Тогда множество точек трехмерного пространства с координатами (x,y,z), где  , является графиком функции двух переменных. Поскольку уравнение (15.1) определяет некоторую поверхность в трехмерном пространстве, она и будет геометрическим изображением рассматриваемой функции.
, является графиком функции двух переменных. Поскольку уравнение (15.1) определяет некоторую поверхность в трехмерном пространстве, она и будет геометрическим изображением рассматриваемой функции.
Область определения функции z = f(x,y) в простейших случаях представляет собой либо часть плоскости, ограниченную замкнутой кривой, причем точки этой кривой (границы области) могут принадлежать или не пренадлежать области определения, либо всю плоскость, либо,наконец, совокупностьнескольких частей плоскости xOy.
 |
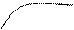

 z
z
z = f(x,y)
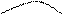
 M y
M y
 |
Примерами могут служить уравнения плоскости z = ax + by + c
и поверхностей второго порядка: z = x ² + y ² (параболоид вращения),
 (конус) и т.д.
(конус) и т.д.

 Замечание. Для функции трех и более переменных будем пользоваться термином «поверхность в n -мерном пространстве», хотя изобразить подобную поверхность невозможно.
Замечание. Для функции трех и более переменных будем пользоваться термином «поверхность в n -мерном пространстве», хотя изобразить подобную поверхность невозможно.
Линии и поверхности уровня
Для функции двух переменных, заданной уравнением (15.1), можно рассмотреть множество точек (х,у) плоскости О ху, для которых z принимает одно и то же постоянное значение, то есть z = const. Эти точки образуют на плоскости линию, называемую линией уровня.
Пример.
Найдем линии уровня для поверхности z = 4 – x ² - y ². Их уравнения имеют вид x ² + y ² = 4 – c (c =const) – уравнения концентрических окружностей с центром в начале координат и с радиусами  . Например, при с =0 получаем окружность x ² + y ² = 4.
. Например, при с =0 получаем окружность x ² + y ² = 4.
Для функции трех переменных u = u (x, y, z) уравнение u (x, y, z) = c определяет поверхность в трехмерном пространстве, которую называют поверхностью уровня.
Пример.
Для функции u = 3 x + 5 y – 7 z –12 поверхностями уровня будет семейство параллельных плоскостей, задаваемых уравнениями 3 x + 5 y – 7 z –12 + с = 0.
Предел и непрерывность функции нескольких переменных
Введем понятие δ-окрестности точки М 0 (х0, у0) на плоскости О ху как круга радиуса δ с центром в данной точке. Аналогично можно определить δ-окрестность в трехмерном пространстве как шар радиуса δ с центром в точке М 0 (х0 , у0, z0). Для n -мерного пространства будем называть δ-окрестностью точки М 0 множество точек М с координатами 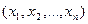 , удовлетворяющими условию
, удовлетворяющими условию
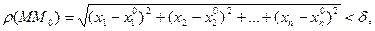
где  - координаты точки М 0. Иногда это множество называют «шаром» в n -мерном пространстве.
- координаты точки М 0. Иногда это множество называют «шаром» в n -мерном пространстве.
Определение. Число А называется пределом функции нескольких переменных f 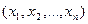 в точке М 0, если
в точке М 0, если 
 такое, что | f(M) – A | < ε для любой точки М из δ-окрестности М 0.
такое, что | f(M) – A | < ε для любой точки М из δ-окрестности М 0.
Обозначения:  .
.
Необходимо учитывать, что при этом точка М может приближаться к М 0, условно говоря, по любой траектории внутри δ-окрестности точки М 0. Поэтому следует отличать предел функции нескольких переменных в общем смысле от так называемых повторных пределов, получаемых последовательными предельными переходами по каждому аргументу в отдельности.
Примеры.
- Покажем, что функция

 не имеет предела при М → О (0,0). Действительно, если в качестве линии, по которой точка М приближается к началу координат, выбрать прямую у = х, то на этой прямой
не имеет предела при М → О (0,0). Действительно, если в качестве линии, по которой точка М приближается к началу координат, выбрать прямую у = х, то на этой прямой 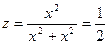 . Если же траекторией движения считать прямую у = 2 х, то
. Если же траекторией движения считать прямую у = 2 х, то 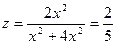 . Следовательно, предел в точке (0,0) не существует.
. Следовательно, предел в точке (0,0) не существует. - Найдем повторные пределы функции
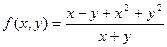 при х→0, у→0.
при х→0, у→0. 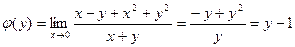 ,
, 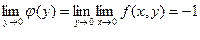 . Если же произвести предельные переходы в обратном порядке, получим:
. Если же произвести предельные переходы в обратном порядке, получим: 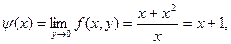
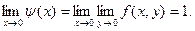 Таким образом, повторные пределы оказались различными (откуда следует, конечно, что функция не имеет в точке (0,0) предела в обычном смысле).
Таким образом, повторные пределы оказались различными (откуда следует, конечно, что функция не имеет в точке (0,0) предела в обычном смысле).
Замечание. Можно доказать, что из существования предела в данной точке в обычном смысле и существования в этой точке пределов по отдельным аргументам следует существование и равенство повторных пределов. Обратное утверждение неверно.
Определение Функция f 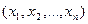 называется непрерывной в точке М 0
называется непрерывной в точке М 0 , если
, если 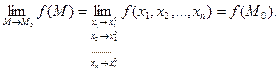 (15.2)
(15.2)
Если ввести обозначения  , то условие (15.2) можно переписать в форме
, то условие (15.2) можно переписать в форме  (15.3)
(15.3)
Определение. Внутренняя точка М0 области определения функции z = f (M) называется точкой разрыва функции, если в этой точке не выполняются условия (15.2), (15.3).
Замечание. Множество точек разрыва может образовывать на плоскости или в пространстве линии или поверхности разрыва.
Примеры.
- Функция z = x ² + y ² непрерывна в любой точке плоскости О ху. Действительно,
 , поэтому
, поэтому 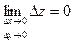 .
. - Единственной точкой разрыва функции
 является точка (0,0).
является точка (0,0). - Для функции
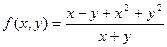 линией разрыва является прямая х + у = 0.
линией разрыва является прямая х + у = 0.
Свойства пределов и непрерывных функций
Так как определения предела и непрерывности для функции нескольких переменных практически совпадает с соответствующими определениями для функции одной переменной, то для функций нескольких переменных сохраняются все свойства пределов и непрерывных функций, доказанные в первой части курса, а именно:
1) Если существуют  то существуют и
то существуют и  (если
(если 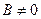 ).
).
2) Если  а
а 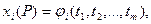 и для любого i существуют пределы
и для любого i существуют пределы  и существует
и существует 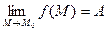 , где М0
, где М0  , то существует и предел сложной функции
, то существует и предел сложной функции 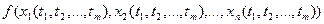 при
при  , где
, где 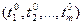 - координаты точки Р 0.
- координаты точки Р 0.
3) Если функции f(M) и g(M) непрерывны в точке М 0, то в этой точке непрерывны и функции f(M) + g(M), kf(M), f(M)•g(M), f(M)/g(M) (если g(M 0) ≠ 0).
4) Если функции  непрерывны в точке Р0
непрерывны в точке Р0 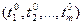 , а функция
, а функция 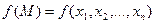 непрерывна в точке М0
непрерывна в точке М0  , где
, где  , то сложная функция
, то сложная функция 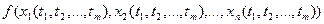 непрерывна в точке Р0.
непрерывна в точке Р0.
5) Функция  непрерывная в замкнутой ограниченной области D, принимает в этой области свое наибольшее и наименьшее значения.
непрерывная в замкнутой ограниченной области D, принимает в этой области свое наибольшее и наименьшее значения.
6) Если функция  непрерывная в замкнутой ограниченной области D, принимает в этой области значения А и В, то она принимает в области D и любое промежуточное значение, лежащее между А и В.
непрерывная в замкнутой ограниченной области D, принимает в этой области значения А и В, то она принимает в области D и любое промежуточное значение, лежащее между А и В.
7) Если функция  непрерывная в замкнутой ограниченной области D, принимает в этой области значения разных знаков, то найдется по крайней мере одна точка из области D, в которой f = 0.
непрерывная в замкнутой ограниченной области D, принимает в этой области значения разных знаков, то найдется по крайней мере одна точка из области D, в которой f = 0.
Частные производные
Рассмотрим изменение функции 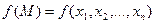 при задании приращения только одному из ее аргументов – хi, и назовем его
при задании приращения только одному из ее аргументов – хi, и назовем его  .
.
Определение. Частной производной функции 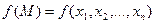 по аргументу хi называется
по аргументу хi называется 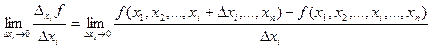 .
.
Обозначения: 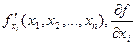 .
.
Таким образом, частная производная функции нескольких переменных определяется фактически как производная функции одной переменной – хi. Поэтому для нее справедливы все свойства производных, доказанные для функции одной переменной.
Замечание. При практическом вычислении частных производных пользуемся обычными правилами дифференцирования функции одной переменной, полагая аргумент, по которому ведется дифференцирование, переменным, а остальные аргументы – постоянными.
Примеры.
1. z = 2 x ² + 3 xy –12 y ² + 5 x – 4 y +2, 
2. z = xy, 
3. 
Геометрическая интерпретация частных производных функции двух переменных
Рассмотрим уравнение поверхности z = f (x,y) и проведем плоскость х = const. Выберем на линии пересечения плоскости с поверхностью точку М (х,у). Если задать аргументу у приращение Δ у и рассмотреть точку Т на кривой с координатами (х, у+ Δ у, z+ Δy z), то тангенс угла, образованного секущей МТ с положительным направлением оси О у, будет равен 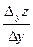 . Переходя к пределу при
. Переходя к пределу при  , получим, что частная производная
, получим, что частная производная  равна тангенсу угла, образованного касательной к полученной кривой в точке М с положительным направлением оси О у. Соответственно частная производная
равна тангенсу угла, образованного касательной к полученной кривой в точке М с положительным направлением оси О у. Соответственно частная производная 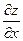 равна тангенсу угла с осью О х касательной к кривой, полученной в результате сечения поверхности z = f (x,y) плоскостью y = const.
равна тангенсу угла с осью О х касательной к кривой, полученной в результате сечения поверхности z = f (x,y) плоскостью y = const.
Дифференцируемость функции нескольких переменных
При исследовании вопросов, связанных с дифференцируемостью, ограничимся случаем функции трех переменных, поскольку все доказательства для большего количества переменных проводятся так же.
Определение. Полным приращением функции u = f(x, y, z) называется
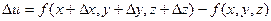 (15.4)
(15.4)
Теорема 1. Если частные производные  существуют в точке (х0, у0, z0) и в некоторой ее окрестности и непрерывны в точке (x0, y0, z0), то
существуют в точке (х0, у0, z0) и в некоторой ее окрестности и непрерывны в точке (x0, y0, z0), то
 , (15.5)
, (15.5)
где α, β, γ – бесконечно малые, зависящие от Δ х, Δ у, Δ z.
Доказательство.
Представим полное приращение Δ u в виде:
 ,
,
где каждая разность представляет собой частное приращение функции только по одной из переменных. Из условия теоремы следует, что к этим разностям можно применить теорему Лагранжа. При этом получим:
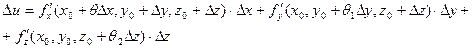 .
.
Так как по условию теоремы частные производные непрерывны в точке (х0, у0, z0), можно представить их в виде:
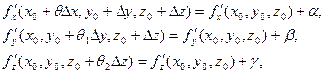
где  . Теорема доказана.
. Теорема доказана.
Можно показать, что  где
где 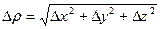 . Действительно, α, β и γ – бесконечно малые при ρ→0, а
. Действительно, α, β и γ – бесконечно малые при ρ→0, а  - ограниченные (т.к. их модули не превышают 1).
- ограниченные (т.к. их модули не превышают 1).
Тогда приращение функции, удовлетворяющей условиям теоремы 1, можно представить в виде: 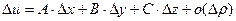 , (15.6)
, (15.6)
где 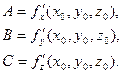 (15.7)
(15.7)
Определение. Если приращение функции u = f (x, y, z) в точке (x0, y0, z0) можно представить в виде (15.6), (15.7), то функция называется дифференцируемой в этой точке, а выражение  - главной линейной частью приращения или полным дифференциалом рассматриваемой функции.
- главной линейной частью приращения или полным дифференциалом рассматриваемой функции.
Обозначения: du, df (x0, y0, z0).
Так же, как в случае функции одной переменной, дифференциалами независимых переменных считаются их произвольные приращения, поэтому

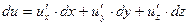 (15.8)
(15.8)
Замечание 1. Итак, утверждение «функция дифференцируема» не равнозначно утверждению «функция имеет частные производные» - для дифференцируемости требуется еще и непрерывность этих производных в рассматриваемой точке.
Замечание 2. Если в формуле (15.8) считать 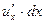 ,
, 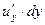 и
и 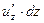 частными дифференциалами данной функции (как функции одного из аргументов), то можно сказать, что полный дифференциал равен сумме частных дифференциалов.
частными дифференциалами данной функции (как функции одного из аргументов), то можно сказать, что полный дифференциал равен сумме частных дифференциалов.
Применение дифференциала к приближенным вычислениям
По аналогии с линеаризацией функции одной переменной можно при приближенном вычислении значений функции нескольких переменных, дифференцируемой в некоторой точке, заменять ее приращение дифференциалом. Таким образом, можно находить приближенное значение функции нескольких (например, двух) переменных по формуле:
 , (15.9)
, (15.9)
где 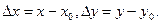
Пример.
Вычислить приближенное значение  .
.
Рассмотрим функцию  и выберем х0 = 1, у0 = 2. Тогда Δ х = 1,02 – 1 = 0,02; Δ у = 1,97 – 2 = -0,03. Найдем
и выберем х0 = 1, у0 = 2. Тогда Δ х = 1,02 – 1 = 0,02; Δ у = 1,97 – 2 = -0,03. Найдем  ,
,
 Следовательно, учитывая, что f ( 1, 2) = 3, получим:
Следовательно, учитывая, что f ( 1, 2) = 3, получим:

|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 12896; Нарушение авторских прав?; Мы поможем в написании вашей работы!