
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференциальные уравнения первого порядка
|
|
|
|
Определение 1. Уравнение вида F(x, y, y')=0, где х — независимая переменная; у — искомая функция; у' — ее производная, называется дифференциальным уравнением первого порядка.
Если уравнение можно разрешить относительно у', то оно принимает вид: y' = f(x,y) и называется уравнением первого порядка, разрешенным относительно производной.
Дифференциальное уравнение удобно записать в виде: 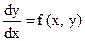 , являющемся частным случаем более общего уравнения (в симметрической форме): P(x,y)dx+Q(x,y)dy =0, где Р (х, у) и Q (х, у) — известные функции.
, являющемся частным случаем более общего уравнения (в симметрической форме): P(x,y)dx+Q(x,y)dy =0, где Р (х, у) и Q (х, у) — известные функции.
Уравнение в симметричной форме удобно тем, что переменные х и у в нем равноправны, т.е. каждую из них можно рассматривать как функцию от другой.
Определение 2. Решением дифференциального уравнения первого порядка называется функция у = j (х), которая при подстановке в уравнение обращает его в тождество.
График решения дифференциального уравнения называется интегральной кривой.
Ответ на вопрос о том, при каких условиях уравнение имеет решение, дает теорема Коши, которая называется теоремой о существовании и единственности решения дифференциального уравнения и является основной в теории дифференциальных уравнений.
Теорема (теорема Коши). Если функция f (x, у) и ее частная производная f'y (x, у) определены и непрерывны в некоторой области G плоскости Оху, то какова бы ни была внутренняя точка (х0; у0) области G, в некоторой окрестности этой точки существует единственное решение уравнения y'=f(x, у), удовлетворяющее условиям: у=уо при х=х0.
Теорема Коши дает возможность по виду дифференциального уравнения решать вопрос о существовании и единственности его решения. Это особенно важно в тех случаях, когда заранее неизвестно, имеет ли данное уравнение решение.
Геометрически теорема утверждает, что через каждую внутреннюю точку (x0; у0) области G проходит единственная интегральная кривая. Очевидно, что в области G уравнение имеет бесконечное число различных решений.
Условия, в силу которых функция у =j(х) принимает заданное значение у0 в заданной точке х0, называют начальными условиями решения.
Отыскание решения уравнения, удовлетворяющего начальным условиям, — одна из важнейших задач теории дифференциальных уравнений. Эта задача называется задачей Коши.
С геометрической точки зрения решить задачу Коши — значит из множества интегральных кривых выделить ту, которая проходит через заданную точку (х0; у0) плоскости Оху.
Точки плоскости, через которые либо проходит более одной интегральной кривой, либо не проходит ни одной интегральной кривой, называются особыми точками данного уравнения.
Определение 3. Общим решением уравнения в некоторой области G плоскости Оху называется функция у =j(х, С), зависящая от х и произвольной постоянной С, если она является решением уравнения при любом значении постоянной С, и если при любых начальных условиях таких, что (х0; у0)Î G, существует единственное значение постоянной С=С0 такое, что функция у=j (х, С0) удовлетворяет данным начальным условиям j (х0, С)=С0.
Определение 4. Частным решением уравнения в области G называется функция у=j (х, С0), которая получается из общего решения у=у(х, С) при определенном значении постоянной С=С0.
Геометрически общее решение представляет собой семейство интегральных кривых на плоскости Оху, зависящее от одной произвольной постоянной С, а частное решение — одну интегральную кривую этого семейства, проходящую через заданную точку (х 0; у0).
Иногда начальные условия называют условиями Коши, а частным решением называют решение какой-нибудь задачи Коши.
Геометрический смысл уравнения. Пусть дано дифференциальное уравнение первого порядка y'=f(x, у) и пусть функция у=j (х) - его решение. График решения представляет собой непрерывную интегральную кривую, через каждую точку которой можно провести касательную. Из уравнения следует, что угловой коэффициент у' касательной к интегральной кривой в каждой ее точке (х; у) равен значению в этой точке правой части уравнения f(x, у). Таким образом, уравнение y' = f(x, у) устанавливает зависимость между координатами точки (х; у) и угловым коэффициентом у' касательной к графику интегральной кривой в той же точке. Зная х и у, можно указать направление касательной к этой интегральной кривой в точке (х; у). Сопоставим каждой точке (х; у) интегральной кривой направленный отрезок, угловой коэффициент которого равен f (х, у). Получим так называемое поле направлений данного уравнения, раскрывающее геометрический смысл дифференциального уравнения первого порядка.
Итак, с геометрической точки зрения уравнение y'=f (x, у) определяет на плоскости Оху поле направлений, а решение этого уравнения — интегральная кривая, направление касательной к которой в каждой точке совпадает с направлением поля в этой точке.
Построив на плоскости поле направлений данного дифференциального уравнения, можно приближенно построить интегральные кривые.
§86 ДУ I порядка. Уравнения с разделяющимися переменными
Если ДУ I имеет вид: Р (х) dx + Q (y) dy =0, в котором Р зависит только от х, а Q зависит только от у, то оно является ДУ I с разделёнными переменными.
Общий интеграл уравнения с разделёнными переменными представляется уравнением:
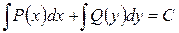
Если ДУ I имеет вид: X 1 Y 1 dy + X 2 Y 2 dx =0, в котором X 1 и X 2 зависят только от х, а Y 1 и Y 2 зависят только от у, то оно является ДУ I с разделяющимися переменными и приводится к ДУ I с разделёнными переменными. Процесс приведения называется разделением переменных.
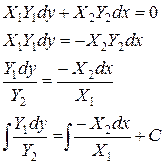
Задание 1. Найти общее решение ДУ I:
у ′ у = x
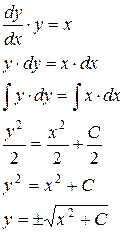 Итак,
Итак, 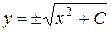 , где C = const – общее решение уравнения.
Найдём частное решение уравнения удовлетворяющее начальным условиям (решим задачу Коши) при у ′ у = x, х 0=2, у 0=0
Получим , где C = const – общее решение уравнения.
Найдём частное решение уравнения удовлетворяющее начальным условиям (решим задачу Коши) при у ′ у = x, х 0=2, у 0=0
Получим 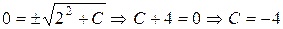 .
Итак, .
Итак,  – частные решения уравнения, удовлетворяющие заданным условиям. – частные решения уравнения, удовлетворяющие заданным условиям.
| у′cosx - ysinx =0
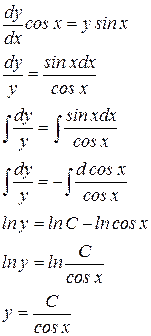 Итак,
Итак, 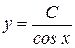 , где C = const – общее решение уравнения. , где C = const – общее решение уравнения.
|
| у ′=-2 xу | у ′=- у 2 |
§87 Однородное ДУ I порядка (ОДУ I)
Пусть ДУ I имеет вид: Мdx + Ndy =0 – оно называется однородным ОДУ I, если отношение M / N можно представить как функцию отношения y / x. Это отношение обозначим через t:

Тогда с помощью данной подстановки ОДУ I приводится к уравнению с разделяющимися переменными.
§88 Линейное ДУ I порядка (ЛДУ I)
Пусть ДУ I имеет вид: Мdx + Ndy =0 – оно называется ЛДУ I, если отношение M/N содержит у лишь в первой степени. ЛДУ I принято записывать в виде у ¢+ Р (x) у = Q (x) где Р (x) и Q (x) непрерывные функции от х.
Если Q (x)=0, то уравнение принимает вид у ¢+ Р (x) у =0 и оно называется ЛОДУ I или линейным уравнением без правой части. В этом случае оно приводится к уравнению с разделяющимися переменными.
Если Q (x)≠0, то уравнение называется ЛНДУ I или линейным уравнением с правой части. В этом случае его можно решить методом Бернулли или методом Лагранжа.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1481; Нарушение авторских прав?; Мы поможем в написании вашей работы!