
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 21. Раскрытие неопределенностей с помощью преобразований
|
|
|
|
При нахождении пределов функций вначале необходимо вместо независимой переменной  подставить ее предельное значение. Если при этом получается конечное значение функции, то оно и будет ее пределом. Если при подстановке выясняется, что возникает неопределенность, то нужно от нее избавиться – раскрыть неопределенность. Для этого раскрытия используются, в первую очередь, два подхода. Первый: преобразование функций, стоящих под знаком предела, с помощью алгебраических и тригонометрических формул. Второй: выделение в рассматриваемой функции некоторых эталонных пределов, называемых замечательными. При раскрытии неопределенностей после каждого преобразования функции в нее подставляют предельное значение переменной, чтобы проверить, осталась ли неопределенность. Действия продолжают до тех пор, пока неопределенность не будет устранена.
подставить ее предельное значение. Если при этом получается конечное значение функции, то оно и будет ее пределом. Если при подстановке выясняется, что возникает неопределенность, то нужно от нее избавиться – раскрыть неопределенность. Для этого раскрытия используются, в первую очередь, два подхода. Первый: преобразование функций, стоящих под знаком предела, с помощью алгебраических и тригонометрических формул. Второй: выделение в рассматриваемой функции некоторых эталонных пределов, называемых замечательными. При раскрытии неопределенностей после каждого преобразования функции в нее подставляют предельное значение переменной, чтобы проверить, осталась ли неопределенность. Действия продолжают до тех пор, пока неопределенность не будет устранена.
Предел дробно-рациональной функции. Прежде чем мы перейдем к разбору возможных преобразований при возникновении неопределенностей отметим еще раз тот факт, что в области непрерывности любой функции её предел равен значению функции в указанной предельной точке, т.е. при отыскании предела дробно-рациональной функции можно в аналитическом выражении функции заменить аргумент его предельным значением, если при этом предельном значении знаменатель не обращается в нуль. Если  , то
, то 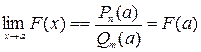 , при
, при  .
.
Пример 1: Найти  .
.
Функция  - целая рациональная. Заменим в аналитическом выражении функции х его предельным значением и получим:
- целая рациональная. Заменим в аналитическом выражении функции х его предельным значением и получим:  .
.
Пример 2: Найти  .
.
Функция  - дробно-рациональная. Прежде чем заменять в аналитическом выражении функции х его предельным значением, нужно проверить, не обращается ли в нуль знаменатель дроби при х=3. Проверяем:
- дробно-рациональная. Прежде чем заменять в аналитическом выражении функции х его предельным значением, нужно проверить, не обращается ли в нуль знаменатель дроби при х=3. Проверяем:  .
. 
Для самостоятельного решения:
1. Найти 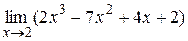 . Ответ: -2.
. Ответ: -2.
2. Найти 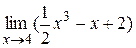 . Ответ:30.
. Ответ:30.
3. Найти 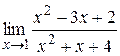 . Ответ: 0.
. Ответ: 0.
4. Найти  . Ответ: -1,5.
. Ответ: -1,5.
Рассмотрим другие возможные случаи, возникающие при отыскании предела дробно-рациональной функции. Так, например, если  ,
,  , то частное
, то частное 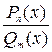 дает неопределенность
дает неопределенность . Для того, чтобы определить предел дробно-рациональной функции в этом случае, нужно числитель и знаменатель дроби разделить на (х-а) и перейти к пределу. Если и после этого числитель и знаменатель новой дроби имеют пределы, равные нулю при
. Для того, чтобы определить предел дробно-рациональной функции в этом случае, нужно числитель и знаменатель дроби разделить на (х-а) и перейти к пределу. Если и после этого числитель и знаменатель новой дроби имеют пределы, равные нулю при  , то надо произвести повторное деление на (х-а). Другими словами эта неопределенность вида
, то надо произвести повторное деление на (х-а). Другими словами эта неопределенность вида  , заданная отношением двух многочленов раскрывается разложением многочленов на множители и сокращением общих множителей в числителе и знаменателе.
, заданная отношением двух многочленов раскрывается разложением многочленов на множители и сокращением общих множителей в числителе и знаменателе.
Пример 3: Найти 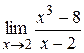 .
.
 .
.
Пример 4. Найти 

Пример 5. Найти 

Для самостоятельного решения:
1. Найти  . Ответ:
. Ответ:  .
.
2. Найти  . Ответ:
. Ответ:  .
.
3. Найти  . Ответ:
. Ответ:  .
.
4. Найти  . Ответ:
. Ответ:  .
.
Другой вид неопределенности  дает
дает  где
где  и
и  – многочлены. В этом случае мы имеем дело с отношением двух бесконечно больших функций. Без специального исследования об этом отношении нельзя сказать ничего определенного.
– многочлены. В этом случае мы имеем дело с отношением двух бесконечно больших функций. Без специального исследования об этом отношении нельзя сказать ничего определенного.
Пусть  - многочлен степени n, а
- многочлен степени n, а  - многочлен степени m. Нам требуется найти
- многочлен степени m. Нам требуется найти
 .
.
Вынесем за скобку в числителе  , а в знаменателе
, а в знаменателе :
:

Таким образом, для нахождения предела функции в данном случае следует разделить числитель и знаменатель дроби на высшую степень х, встречающуюся в членах дроби, а после этого перейти к пределу.
Пример 6: Найти 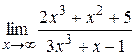 .
.
Разделим числитель и знаменатель дроби на 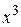 .
.
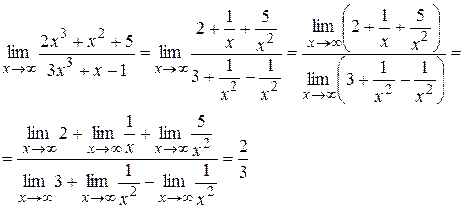
так как при  функции
функции 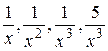 являются бесконечно малыми (т.е. пределы их равны нулю).
являются бесконечно малыми (т.е. пределы их равны нулю).
Пример 6. Найти  .
.
Разделим числитель и знаменатель дроби на  .
.

Пример 7. Найти  .
.
Разделим числитель и знаменатель дроби на 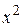 .
.

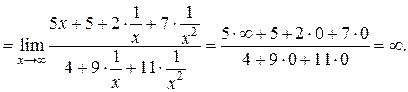
Правило. Предел неопределенности вида 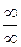 , заданной отношением двух многочленов, равен:
, заданной отношением двух многочленов, равен:
а) нулю, если максимальная степень независимой переменной x в знаменателе больше, чем максимальная степень  в числителе;
в числителе;
б) ± бесконечности, если максимальная степень  в числителе больше, чем в знаменателе (+¥, если коэффициенты при максимальных степенях в числителе и знаменателе одного знака, –¥, если указанные коэффициенты разных знаков);
в числителе больше, чем в знаменателе (+¥, если коэффициенты при максимальных степенях в числителе и знаменателе одного знака, –¥, если указанные коэффициенты разных знаков);
в) отношению коэффициентов при максимальных степенях, если они одинаковы в числителе и знаменателе.
Для самостоятельного решения:
1. Найти  . Ответ:5
. Ответ:5
2. Найти  . Ответ:
. Ответ:  .
.
3. Найти  . Ответ:0
. Ответ:0
4. Найти 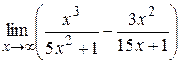 . Ответ:
. Ответ:  .
.
Предел дроби, содержащей иррациональные выражения. В этом случае может возникнуть два вида неопределенностей:  - когда пределы числителя и знаменателя дроби равны нулю, и
- когда пределы числителя и знаменателя дроби равны нулю, и  - когда пределы числителя и знаменателя дроби равны бесконечности.
- когда пределы числителя и знаменателя дроби равны бесконечности.
Чтобы найти предел дроби, содержащей иррациональные выражения в первом случае, надо перенести иррациональность из числителя в знаменатель или из знаменателя в числитель с помощью умножения числителя и знаменателя на соответствующие алгебраические выражения. После этого выполнить все возможные упрощения и перейти к пределу.
Пример 8: Найти 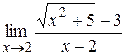 .
.
При  числитель и знаменатель дроби имеют предел, равный нулю. Перенесем иррациональность в знаменатель. Для этого умножим числитель и знаменатель на выражение
числитель и знаменатель дроби имеют предел, равный нулю. Перенесем иррациональность в знаменатель. Для этого умножим числитель и знаменатель на выражение  , сопряженное к числителю. Оно необходимо для представления числителя по формуле разности квадратов двух выражений.
, сопряженное к числителю. Оно необходимо для представления числителя по формуле разности квадратов двух выражений.

Пример 9: Найти  .
.
При  числитель и знаменатель дроби имеют предел, равный нулю. В этой задаче придется сначала числитель и знаменатель дроби умножить на
числитель и знаменатель дроби имеют предел, равный нулю. В этой задаче придется сначала числитель и знаменатель дроби умножить на  , а потом на
, а потом на  .
.

Пример 10. Найти 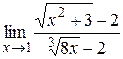 .
.
При  числитель и знаменатель дроби имеют предел, равный нулю. В этой задаче придется сначала числитель и знаменатель дроби умножить на
числитель и знаменатель дроби имеют предел, равный нулю. В этой задаче придется сначала числитель и знаменатель дроби умножить на  , дополняя тем самым числитель до полного квадрата, а потом на
, дополняя тем самым числитель до полного квадрата, а потом на 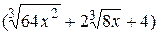 , дополняя знаменатель до разности кубов.
, дополняя знаменатель до разности кубов.

Для самостоятельного решения:
1. Найти  . Ответ:
. Ответ:  .
.
2. Найти 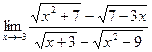 . Ответ: 0.
. Ответ: 0.
3. Найти  . Ответ:
. Ответ:  .
.
4. Найти  . Ответ:
. Ответ:  .
.
Чтобы найти предел дроби, содержащей иррациональные выражения в случае неопределенности  , нужно использовать прием, описанный для дробно-рациональных функций. Различие заключается в том, что здесь многочлены, как правило, стоят под знаком корня, поэтому деление числителя и знаменателя дроби на высшую степень х следует производить с подкоренными выражениями.
, нужно использовать прием, описанный для дробно-рациональных функций. Различие заключается в том, что здесь многочлены, как правило, стоят под знаком корня, поэтому деление числителя и знаменателя дроби на высшую степень х следует производить с подкоренными выражениями.
Пример 10: Найти  .
.

В этом случае, так же как и для дробно-рациональных функций, можно предсказать вероятное значение предела по максимальным степеням числителя и знаменателя. При определении максимальных степеней следует пользоваться тем фактом, что при  выражение
выражение  можно представить следующим образом:
можно представить следующим образом:  , где под многоточием предполагается бесконечно большая величина при
, где под многоточием предполагается бесконечно большая величина при 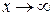 более низшего порядка чем
более низшего порядка чем  .
.
Пример 11: Найти  .
.
Посмотрим, что должно получиться:

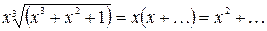 . В итоге знаменатель:
. В итоге знаменатель:

Естественно ожидать, что предел будет равен 1/3.

Для самостоятельного решения:
1. Найти  . Ответ:
. Ответ: 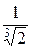 .
.
2. Найти  . Ответ: 0.
. Ответ: 0.
3. Найти  . Ответ: 0.
. Ответ: 0.
4. Найти  . Ответ:
. Ответ:  .
.
Существует еще один тип пределов вида 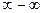 , которые можно свести к рассмотренным пределам, содержащим иррациональные выражения в случае неопределенности
, которые можно свести к рассмотренным пределам, содержащим иррациональные выражения в случае неопределенности  . Способов сведения два:
. Способов сведения два:
1) перенести иррациональность из числителя в знаменатель;
2) использовать формулы сокращенного умножения для уничтожения разности квадратных и кубических корней.


Пример 12: Найти  .
.
Для того, чтобы избавиться от разности с квадратным корнем, умножим и поделим всю разность на сопряженное ей выражение.
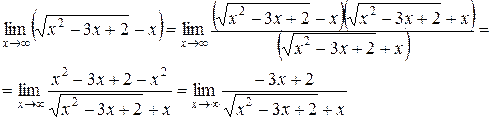
Таким образом, мы свели задачу к предыдущей. Далее, определив степень числителя и знаменателя, поделим числитель и знаменатель на х и в результате получим:
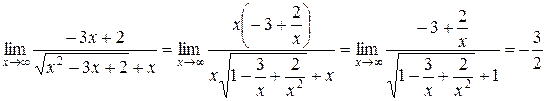
Для самостоятельного решения:
1. Найти  . Ответ:-2,5.
. Ответ:-2,5.
2. Найти  . Ответ:
. Ответ:  .
.
3. Найти  . Ответ: 0.
. Ответ: 0.
4. Найти  . Ответ: 0.
. Ответ: 0.
Вычисление пределов выражений, содержащих показательные и логарифмические функции. В этих случаях при определенных условиях можно обойти сложности от появления показательной или логарифмической функции простым выносом самой функции за знак предела. Так, например, если существует предел  и этот предел положителен, то
и этот предел положителен, то  . Другими словами, можно переходить к пределу под знаком логарифма. Требование, что
. Другими словами, можно переходить к пределу под знаком логарифма. Требование, что связано с тем, что число А в правой части формулы стоит под знаком логарифма, а логарифмическая функция определена только для положительных значений аргумента.
связано с тем, что число А в правой части формулы стоит под знаком логарифма, а логарифмическая функция определена только для положительных значений аргумента.
Для показательной функции вынос самой функции за знак предела происходит аналогично, с той разницей, что в этом случае не требуется никаких условий на знак  . Как следствием вышесказанного, полезно пользоваться следующим фактом: если
. Как следствием вышесказанного, полезно пользоваться следующим фактом: если 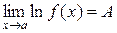 , то
, то  . Этот факт используется при сведении неопределенностей
. Этот факт используется при сведении неопределенностей  к неопределенностям вида
к неопределенностям вида  с помощью логарифмирования функции. Об этом мы расскажем позднее при изучении правила Лопиталя.
с помощью логарифмирования функции. Об этом мы расскажем позднее при изучении правила Лопиталя.
Пример 13: Найти  .
.
 .
.
Пример 14: Найти  .
.

Пример 15: Найти 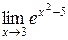 .
.
 .
.

|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 3901; Нарушение авторских прав?; Мы поможем в написании вашей работы!