Маршруты и связность

Матрица инцидентности

Матрица смежности

Матрица смежности — таблица, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).

Недостатком являются требования к памяти — очевидно, квадрат количества вершин.

- двумерный массив;

- матрица с пропусками;

- не явное задание (при помощи функции).

Каждая строка соответствует определённой вершине графа, а столбцы соответствуют связям графа. В ячейку на пересечении i-ой строки с j-м столбцом матрицы записывается:

1 - в случае, если связь j «выходит» из вершины i,

−1 - если связь «входит» в вершину,

0 - во всех остальных случаях (т.е. если связь является петлёй или связь не инцидентна вершине)

Данный способ является самым ёмким и неудобным для хранения, но облегчает нахождение циклов в графе.

Список рёбер — это тип представления графа в памяти, подразумевающий, что каждое ребро представляется двумя числами — номерами вершин этого ребра. Список рёбер более удобен для реализации различных алгоритмов на графах по сравнению с матрицей смежности.

Обычно в теории графов выделяют некоторые разновидности графов. Среди таких разновидностей выделим следующие:

- полный граф - граф, матрица смежности которого состоит из одних единиц;

- полный обыкновенный граф - граф, у матрицы смежности которого все элементы, за исключением нулевых элементов главной диагонали, равны единице;

- пустой (нулевой) граф - граф, матрица смежности которого нулевая (обыкновенный граф, все вершины которого изолированы, т.е. нет ни одной пары смежных вершин);

- единичный граф - граф, матрица смежности которого единичная (граф, все вершины которого имеют петли и изолированы);

- плоский (планарный) граф - граф, который можно начертить на плоскости так, чтобы его ребра (дуги) пересекались только в его вершинах.

Одно из наиболее простых свойств, которым может обладать граф, это свойство быть связным. Маршрутом в графе G называется чередующаяся последовательность вершин и ребер.

Замкнутый маршрут называется простым циклом, если все его n вершин различны и n³3.

Рис. 2. Граф для иллюстрации маршрутов

В помеченном графе G на рис. 2 v₀v₁v₂…v_n – маршрут, который не является цепью, v₁v₂v₅v₄v₂v₃ – сложная цепь, v₁v₂v₅v₄ – простая цепь, v₂v₄v₅v₂ – простой цикл.

Обозначим через G_n граф, состоящий из одного простого цикла с n вершинами, и через простую цепь с n вершинами; часто называют треугольником. Граф G называется связным, если любая пара его вершин соединена простой цепью. Максимальный связный подграф графа G, называется компонентой связности, или просто компонентой графа G.

Таким образом, несвязный граф имеет, по крайней мере, две компоненты. Граф на рис. 3 имеет 10 компонент.

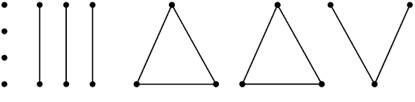
Рис. 3. Граф с 10 компонентами

Расстоянием d(u,v) между двумя вершинами u и v графа G называется длина кратчайшей простой цепи, соединяющей их; если u и v не соединены, то полагаем d(u,v)=µ.

Нарисуем теперь два графа: полный обыкновенный граф К₅ и полный двудольный граф К_3,3 ввиду их особой значимости.

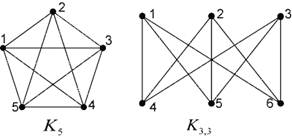
Рис. 5.

Выпишем также их матричные представления:

, .

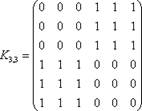Используя введенные выше обозначения, с графом G, заданным матрицей A, можем связать матрицу 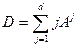, которую будем называть матрицей расстояний. Матрица D, вообще говоря, не будет (0,1)-матрицей, у этой матрицы на месте (u,v) будет стоять число d(u,v), поэтому она и называется матрицей расстояний.

Для графа на рисунке 2 его матрицы A и D будут иметь вид:

,

По матрице D легко определяется диаметр графа d, как максимальное значение элементов этой матрицы. В приведенном примере d=2.

В ографе степень исхода вершины совпадает со степенью захода вершины и называется просто степенью вершины. Вершины со степенью, равной 1, называются висячими. Степень вершины v обозначают как deg v.

Ограф называется ациклическим, если в нем нет циклов. Дерево — это связный ациклический ограф. Каждый ограф, не содержащий циклов, называется лесом. Компонентами леса являются деревья.

Деревом называется связный ограф, у которого число ребер на единицу меньше числа вершин.

Для избежания противоречий под деревом мы будем понимать ограф с числом вершин n, где n³2.

В любом дереве имеются, по крайней мере, две висячие вершины.

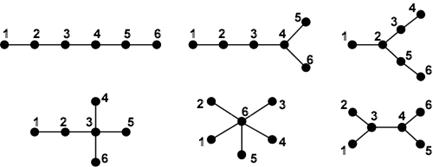
Рисунок 6.

Матрицы деревьев изображенных на рисунке 6:

,,,

,,.

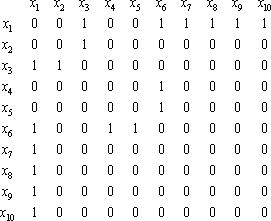
Рис.7(а) Дерево

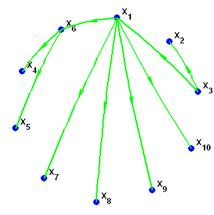
Рис.7(б) Ориентированное выходящее дерево (вершина x₃)

Рис.7(в) Ориентированное входящее дерево (вершина x₃)

Каждое ребро ограничивается двумя вершинами.

Вершина, ограничивающая некоторое ребро, называется инцидентной этому ребру.

Два ребра называются смежными, если они инцидентны одной и той же вершине.

Так на рисунках 1 и 2 даны по два представления одного и того же графа.

Рисунок 1.

Рисунок 2.

Тогда два представления графа с рисунка 1 будут заданы двумя списками:

1 2, 3, 4 I II, III, V

2 3 II IV

3 4 III V

4 5 IV I

5 1 V II

Два представления графа с рисунка 2 будут заданы списками:

1 2, 3, 4, 5 I II, III, IV, V

2 1, 3 II I, IV, V

3 1, 2, 4 III I, V

4 1, 3, 5 IV I, II

5 1, 4 V I, II, III

В первых столбцах таблиц - первые элементы пар, затем по строкам, списком, через запятую, идут вторые элементы.

Два представления графа с рисунка 2 будут заданы также своими множествами X:и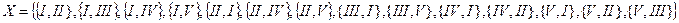

Третье задание графа - матрицами. Ниже, в соответствии с матричным определением 1, выписаны две матрицы смежности – А₁ и А₂, задающие два представления графа с рисунка 1:

и две матрицы смежност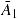и и , задающие два представления графа с рисунка 2:

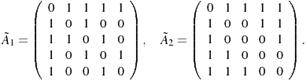
Кроме того, графы с рисунка 2 могут быть заданы своими матрицами инциденци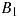й и :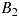

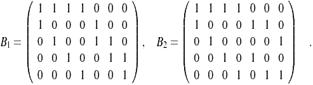
(Нумерация ребер произведена в том порядке, в котором пары, задающие ребра, выписаны в соответствующих множествах ).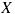

Контрольные вопросы

1. Дать определение графа в геометрической терминологии и его основным компонентам.
2. Дать определение графа в теоретико-множественной терминологии и его основным компонентам.
3. Дать определение графа в матричной терминологии и его основным компонентам.
4. Дать определение матрице смежности. Как формируется матрица? Примеры.
5. Дать определение матрице инцидентности. Как формируется матрица? Примеры.
6. Дать определение матрице расстояний. Как формируется матрица? Примеры.
7. Дать определение матрице деревьев. Как формируется матрица? Примеры.
8. Как представить граф множеством?

Дата добавления: 2014-01-04