
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 21 Колебательное и вращательное движение двухатомных молекул
|
|
|
|
1 Модель гармонических колебаний двухатомной молекулы
2 Колебательный спектр двухатомной молекулы в ангармоническом приближении
3 Описание вращательного движения линейных молекул в приближении жесткого ротатора
4 Учет центробежного растяжения молекулы при ее вращении
Наряду с движением электронов, рассмотренным выше, в молекуле совершается также движение ядер. Их движение, называемое ядерным движением, в приближении Борна-Оппенгеймера можно представить как суперпозицию колебательного и вращательного движения.
Колебательным движением молекулы называют периодическое изменение взаимного расположения ядер молекулы, при котором изменяются межъядерные расстояния и валентные углы. Квантовые переходы, соответствующие колебательному движению, проявляются в спектрах поглощения и испускания (соответствующее им излучение локализовано в ближней инфракрасной области) и в спектрах комбинационного рассеяния, расположенных в ультрафиолетовой и видимой области электромагнитного излучения.
Рассмотрим квантово-механическое описание колебательного движения двухатомных молекул. Запишем стационарное уравнение Шрёдингера для колебательного движения молекулы
 , (22.1)
, (22.1)
где  – оператор полной энергии колебательного движения (оператор Гамильтона),
– оператор полной энергии колебательного движения (оператор Гамильтона), 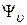 и
и  – собственная функция и собственное значение оператора
– собственная функция и собственное значение оператора  .
.
Опишем колебательное движение двухатомной молекулы в системе координат, начало которой совмещено с центром масс молекулы (рисунок 22.1). На рисунке 22.1 рядом с положением массы ядер молекулы указаны их массы m 1 и m 2; r 1 и r 2 – модули радиус-векторов, определяющих положение ядер в системе центра масс, положение которого обозначено цифрой 0. Обозначим межъядерное расстояние в молекуле 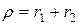 .
.
 |
Колебательное движение двухатомной молекулы состоит в периодическом изменении ее межъядерного расстояния  . Следовательно, рассматриваемая задача является одномерной. Проанализируем вид оператора Гамильтона
. Следовательно, рассматриваемая задача является одномерной. Проанализируем вид оператора Гамильтона
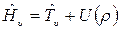 . (22.2)
. (22.2)
Оператор кинетической энергии колебательного движения молекулы имеет вид:
 , (22.3)
, (22.3)
где  – приведенная масса молекулы,
– приведенная масса молекулы,  – отличие межъядерного расстояния от его равновесного значения
– отличие межъядерного расстояния от его равновесного значения  , при котором потенциальная энергия молекулы
, при котором потенциальная энергия молекулы  минимальна.
минимальна.
В качестве потенциальной энергии колебательного движения ядер молекулы  следует рассматривать полную энергию электронов
следует рассматривать полную энергию электронов  (электронную энергию). Действительно, при смещении ядер из положения равновесия силы химической связи стремятся вернуть их в исходное положение. Так как химическая связь определяется движением электронов, естественно, что возвращающая сила возникает вследствие изменения электронной энергии, которая и имеет смысл потенциальной энергии колебания
(электронную энергию). Действительно, при смещении ядер из положения равновесия силы химической связи стремятся вернуть их в исходное положение. Так как химическая связь определяется движением электронов, естественно, что возвращающая сила возникает вследствие изменения электронной энергии, которая и имеет смысл потенциальной энергии колебания  .
.
Вопрос об аналитическом виде кривых  двухатомных молекул в широкой области значений
двухатомных молекул в широкой области значений  достаточно сложен. Вместе с тем известно, что эти кривые обладают минимумом при расстоянии между ядрами
достаточно сложен. Вместе с тем известно, что эти кривые обладают минимумом при расстоянии между ядрами  , называемом равновесным межъядерным расстоянием. Поэтому при квантово-механическом описании колебательного движения молекулы определяют изменение ее колебательной энергии относительно энергии в равновесном состоянии.
, называемом равновесным межъядерным расстоянием. Поэтому при квантово-механическом описании колебательного движения молекулы определяют изменение ее колебательной энергии относительно энергии в равновесном состоянии.
В общем случае под равновесной конфигурацией молекулы понимается такое расположение ее ядер, которое соответствует минимуму энергии молекулы в данном электронном состоянии. Для двухатомной молекулы функцию  независимо от вида её можно разложить в ряд в окрестности
независимо от вида её можно разложить в ряд в окрестности  по параметру
по параметру  . При этом получим
. При этом получим
 (22.4)
(22.4)
Величина  называется колебательной координатой.
называется колебательной координатой.
Так как  , то при малых амплитудах колебаний, т.е. при малых значениях
, то при малых амплитудах колебаний, т.е. при малых значениях  выражение (22.4) можно представить в виде
выражение (22.4) можно представить в виде
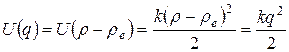 , (22.5)
, (22.5)
где
 (22.6)
(22.6)
– силовая постоянная химической связи.
Вид потенциальной кривой, соответствующей такому приближению, приведен на рисунке 22.2.
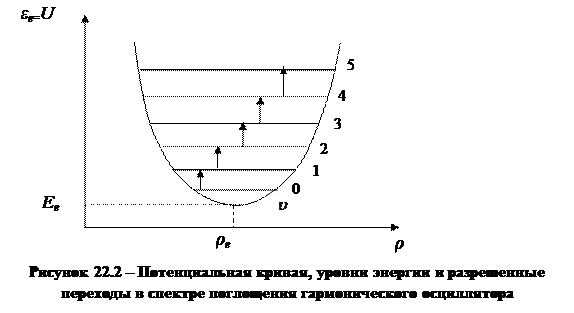 |
Из формулы (22.5) следует, что при небольших амплитудах колебаний (небольших смещениях ядер) реальная кривая  с хорошей точностью аппроксимируется кривой параболического типа. Иначе говоря, малые колебания двухатомных молекул могут рассматриваться как колебания гармонического осциллятора.
с хорошей точностью аппроксимируется кривой параболического типа. Иначе говоря, малые колебания двухатомных молекул могут рассматриваться как колебания гармонического осциллятора.
Таким образом, чтобы описать состояние колебательного движения двухатомной молекулы методами квантовой механики, необходимо решить стационарное уравнение Шрёдингера (22.1), в котором после учета выражений (22.2), (22.3), (22.5) гамильтониан может быть представлен в виде:
 . (22.7)
. (22.7)
Сформулированная задача идентична модельной квантово-механической задаче о гармоническом осцилляторе (смотри лекцию 7). Ее решением является собственная функция
 , (22.8)
, (22.8)
где  - полином Эрмита
- полином Эрмита  -й степени,
-й степени, 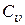 - нормировочные коэффициенты,
- нормировочные коэффициенты,  , и собственные значения энергии колебательного движения
, и собственные значения энергии колебательного движения
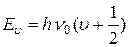 . (22.9)
. (22.9)
Здесь
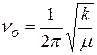 (22.10)
(22.10)
– собственная частота колебания молекулы;  – колебательное квантовое число, его возможные значения – положительные целые числа:
– колебательное квантовое число, его возможные значения – положительные целые числа:  = 0, 1, 2….
= 0, 1, 2….
Воспользуемся формулой (22.9) и дополнительно к потенциальной кривой изобразим на рисунке 22.2 схему колебательных уровней двухатомной молекулы.
Вычисляя матричный элемент оператора дипольного момента (eq) для колебательного перехода из состояния, которому соответствует волновая функция  , в состояние, описываемое волновой функцией
, в состояние, описываемое волновой функцией  , –
, –
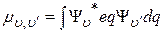 ,
,
можно получить правила отбора для разрешенных переходов (соответствующий им матричный элемент отличен от нуля):
 . (22.11)
. (22.11)
В инфракрасной (ИК) области исследуют, как правило, спектры поглощения (рисунок 22.2). Выразим частоту излучения, поглощаемого при разрешенных переходах, сопровождающихся ИК поглощением, применяя правило частот Бора:
 . (22.12)
. (22.12)
Таким образом, в соответствии с моделью гармонического осциллятора колебательный спектр двухатомной молекулы содержит только одну спектральную линию; частота соответствующего ей излучения равна частоте собственных колебаний молекулы.
Отметим, что проведенное описание не является полностью адекватным реальным двухатомным молекулам. Их экспериментально изученные колебательные спектры имеют более сложную структуру. Кроме того, в рамках модели гармонических колебаний невозможно объяснить такое важное явление как диссоциация молекулы. Для объяснения этих фактов требуется использовать более общую модель колебательного движения.
Как отмечалось выше, модель гармонических колебаний приемлема только при малых амплитудах колебаний. При больших амплитудах колебания становятся ангармоническими. Поэтому более общей моделью описания колебательного движения молекулы является модель ангармонических колебаний (ангармонического осциллятора). Используя эту модель, необходимо представлять функцию (22.4), посредством которой описывается потенциальная энергия колебательного движения, в общем виде. В настоящее время известно много разнообразных приближенных формул, с использованием которых описывают реальные зависимости  . Одним из наиболее распространенных выражений такого рода является формула Морзе
. Одним из наиболее распространенных выражений такого рода является формула Морзе
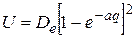 , (22.13)
, (22.13)
где De – энергия диссоциации (энергия, необходимая для того, чтобы разрушить химическую связь в молекуле); а – постоянная для данной молекулы величина, влияющая на форму потенциальной кривой (рисунок 3). Соответствующая (22.13) потенциальная кривая существенно отличается от кривой параболического типа.
Колебательная энергия двухатомной молекулы в ангармоническом приближении определятся следующим образом:
 , (22.14)
, (22.14)
где  – параметр ангармоничности (
– параметр ангармоничности ( ).
).
Как следует из выражения (22.14), колебательные энергетические уровни с увеличением колебательного квантового числа  сгущаются. При достижении колебательной энергией молекулы значения
сгущаются. При достижении колебательной энергией молекулы значения 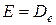 происходит её диссоциация, и спектр энергий образовавшихся при этом атомов сплошной.
происходит её диссоциация, и спектр энергий образовавшихся при этом атомов сплошной.
 |
Правила отбора для колебательных переходов, проявляющихся в ИК и КР спектрах ангармонического осциллятора, имеют вид:
 = ±1, ±2,…
= ±1, ±2,…
Спектральные линии, соответствующие переходам, при которых Δ = ±1, называют основным тоном; соответствующие переходам с
= ±1, называют основным тоном; соответствующие переходам с  , – первым обертоном; соответствующие переходам с
, – первым обертоном; соответствующие переходам с  – вторым обертоном и т.д.
– вторым обертоном и т.д.
Воспользуемся правилом частот Бора и формулой (22.14) для колебательной энергии ангармонического осциллятора и определим частоты спектральных линий в ИК-спектре поглощения, обозначая при этом 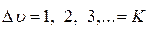 :
:
 . (22.15)
. (22.15)
Таким образом, в сравнении с гармоническим осциллятором в ангармоническом приближении дополнительно к спектральной линии с частотой  , характерной для гармонического осциллятора, возможны спектральные линии, соответствующие переходам, в которых соблюдаются правилами отбора
, характерной для гармонического осциллятора, возможны спектральные линии, соответствующие переходам, в которых соблюдаются правилами отбора  = ±2, ±3,... Вследствие этого в спектре наблюдаются обертонные частоты. В результате теоретического расчета показано, что вероятность разрешенных колебательных переходов при увеличении
= ±2, ±3,... Вследствие этого в спектре наблюдаются обертонные частоты. В результате теоретического расчета показано, что вероятность разрешенных колебательных переходов при увеличении  быстро уменьшается. Следовательно, интенсивность спектральных линий основного тона значительно выше, чем интенсивность первого и, тем более, второго обертона.
быстро уменьшается. Следовательно, интенсивность спектральных линий основного тона значительно выше, чем интенсивность первого и, тем более, второго обертона.
Вид модельного колебательного спектра поглощения двухатомной молекулы, рассчитанного в приближении ангармонического осциллятора, приведен на рисунке 22.4.
 |
На рисунке 22.4 представлено схематическое изображение колебательного спектра поглощения, обусловленного переходами с различных колебательных уровней (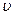 = 0, 1, 2). Интенсивность спектральных линий колебательного спектра в пределах каждого тона быстро уменьшается с ростом колебательного квантового числа
= 0, 1, 2). Интенсивность спектральных линий колебательного спектра в пределах каждого тона быстро уменьшается с ростом колебательного квантового числа 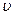 . Этот факт объясняется тем, что в условиях термодинамического равновесия заселенность колебательных уровней молекулами при увеличении энергии уменьшается по экспоненциальному закону. При идентификации экспериментальных спектров поглощения с достаточной точностью можно ограничиться рассмотрением спектральных линий, указанных в таблице 22.1.
. Этот факт объясняется тем, что в условиях термодинамического равновесия заселенность колебательных уровней молекулами при увеличении энергии уменьшается по экспоненциальному закону. При идентификации экспериментальных спектров поглощения с достаточной точностью можно ограничиться рассмотрением спектральных линий, указанных в таблице 22.1.
Таблица 22.1 – Основной и первые обертоны колебательного спектра поглощения двухатомной молекулы (приближение ангармонического осциллятора)
| Переход | Название тона | Частота поглощаемого излучения | Интенсивность линии поглощения |

| Основной тон | 
| Высокая |
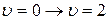
| Первый обертон | 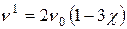
| Низкая |
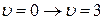
| Второй обертон | 
| Очень низкая |
Полученные результаты находятся в хорошем соответствии с экспериментальными данными о колебательных спектрах различных двухатомных молекул, что является доказательством адекватности рассмотренного здесь квантово-механического описания колебательного движения таких молекул.
Для молекулы возможны два основных вида вращательного движения: вращение молекулы как целого вокруг некоторого направления (оси вращения) или точки (центра вращения) и вращение одних частей молекулы относительно других её частей – внутреннее вращение. Внутреннее вращение молекулы обычно затруднено наличием потенциального барьера между различными положениями равновесия при вращении, соответствующими определенной симметрии молекул. Если это вращение практически невозможно, допустимо только кручение молекулы, сопровождаемое крутильными колебаниями. Если энергия крутильных колебаний достаточно велика, то молекула может преодолеть потенциальный барьер и перейти в соседнее равновесное состояние.
Рассмотрим квантово-механическое описание вращательного движения молекулы как целого, не учитывая внутреннего вращения. Отметим, что при описании движения молекул в дипольном приближении в соответствии с правилами отбора в их спектрах проявляются только те квантовые переходы, при которых изменяется вектор дипольного момента молекулы. Вращательное движение молекулы, состоящее в периодическом изменении ориентации в пространстве молекулы как целого, не сопровождается изменением модуля дипольного момента, а обусловливает только изменение его направления. Поэтому свободные от влияния других движений (так называемые чистые) вращательные спектры характерны для молекул, дипольный момент которых отличен от нуля.
Рассмотрим двухатомную молекулу ХУ, связывая с ней систему главных осей инерции (рисунок 22.5). Начало этой системы совместим с центром инерции молекулы.
Видим, что вращение относительно оси а не обусловливает изменения ориентации молекулы в пространстве, поэтому вращение двухатомной молекулы (как и любой линейной молекулы) характеризуется двумя степенями свободы. Моменты инерции молекулы относительно осей b и c одинаковы и определяются в соответствии с формулой
 . (22.16)
. (22.16)
С учетом соотношений  и
и  получим:
получим:
 , (22.17)
, (22.17)
где  – приведенная масса молекулы.
– приведенная масса молекулы.
 |
Так как для жесткого ротатора  , можно считать, что потенциальная энергия вращательного движения
, можно считать, что потенциальная энергия вращательного движения  равна нулю. При этом условии уравнение Шрёдингера для жесткого ротатора, совершающего вращательное движение относительно одной оси, имеет вид:
равна нулю. При этом условии уравнение Шрёдингера для жесткого ротатора, совершающего вращательное движение относительно одной оси, имеет вид:
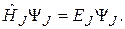 (22.18)
(22.18)
Оператор Гамильтона здесь тождественен оператору кинетической энергии, обусловленной вращательным движением молекулы:
 , (22.19)
, (22.19)
где
 (22.20)
(22.20)
- оператор, сопоставляемый квадрату модуля вращательного момента импульса молекулы;
 (22.21)
(22.21)
- угловая составляющая оператора Лапласа в сферической системе координат.
 С учетом выражений (22.19), (22.20) уравнение Шрёдингера приведём к виду:
С учетом выражений (22.19), (22.20) уравнение Шрёдингера приведём к виду:
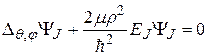 . (22.22)
. (22.22)
Это уравнение аналогично уравнению для угловой части волновой функции водородоподобной атомной системы и решения имеют вид:
 , (22.23)
, (22.23)
где 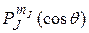 - присоединенные полиномы Лежандра.
- присоединенные полиномы Лежандра.
При этом дискретный спектр собственных значений энергии вращения молекулы определяется по формуле
 , (22.24)
, (22.24)
где
 (22.25)
(22.25)
– вращательная постоянная.
В формулах (22.23), (22.24)  - вращательное квантовое число, содержащееся также в законе квантования модуля вращательного момента молекулы:
- вращательное квантовое число, содержащееся также в законе квантования модуля вращательного момента молекулы:
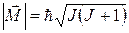 . (22.26)
. (22.26)
Проекции вращательного момента молекулы на направление оси, относительно которой совершается вращение молекулы, квантованы по правилу
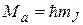 , (22.27)
, (22.27)
где 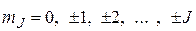 - квантовое число, определяющее значения указанных проекций. Число возможных проекций равно 2J + 1.
- квантовое число, определяющее значения указанных проекций. Число возможных проекций равно 2J + 1.
Линии поглощения, локализованные в микроволновой области спектра, соответствуют квантовым переходам, в которых реализуется правило отбора  , следовательно, в микроволновом спектре молекулы возможны переходы с поглощением излучения, частота которого
, следовательно, в микроволновом спектре молекулы возможны переходы с поглощением излучения, частота которого
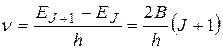 . (22.28)
. (22.28)
Вращательному спектру комбинационного рассеяния соответствуют изменения квантового состояния молекулы, при которых реализуются правила отбора 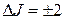 , и смещение линии в спектре комбинационного рассеяния, обусловленное вращательным переходом, определяется следующим образом:
, и смещение линии в спектре комбинационного рассеяния, обусловленное вращательным переходом, определяется следующим образом:
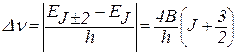 . (22.29)
. (22.29)
Более точное описание вращательных спектров выполняется на основе модели нежесткого ротатора, в которой учитывается деформация молекулы, обусловленная ее центробежным растяжением.
Влияние центробежного растяжения, усиливающегося при увеличении вращательной энергии, учитывается посредством введения поправки в формулу (22.24):
 , (22.30)
, (22.30)
где 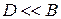 – вращательная постоянная, учитывающая центробежное растяжение молекулы.
– вращательная постоянная, учитывающая центробежное растяжение молекулы.
В результате центробежного растяжения молекулы энергетические уровни понижаются, при этом смещение энергетических уровней тем больше, чем больше значение вращательного квантового числа J.
С учетом центробежного растяжения молекулы изменяются выражения для частоты спектральных линий в инфракрасной области спектра поглощения и смещения частоты в спектре комбинационного рассеяния – формулам (22.28) и (22.29) соответствуют выражения
 , (22.31)
, (22.31)
 . (22.32)
. (22.32)
Реальная молекула совершает одновременно и электронное, и колебательное, и вращательное движение, поэтому полную энергию молекулы (в системе ее центра масс) в адиабатическом приближении можно представить в виде суммы соответствующих парциальных составляющих:
 .
.
Так как парциальные составляющие энергии, соответствующие каждому виду движения молекулы, как показано выше, квантованы, полный спектр возможных значений энергии удобно представить в виде диаграммы энергетических уровней. Изменения энергии в результате квантовых переходов неодинаковы в системе уровней различного типа (электронных, колебательных, вращательных), соответствующие им величины соотносятся следующим образом:
 .
.
На рисунке 22.6 без соблюдения масштаба изображена модельная схема энергетических уровней двухатомной молекулы и показаны стрелками квантовые переходы, обусловливающие формирование молекулярных спектров различного типа.
Вращательные переходы молекулы, объединенные на схеме в группу I,сопровождаются изменением энергии на величину ~10-4 эВ и при поглощении и испускании электромагнитного излучения проявляются в далекой инфракрасной и микроволновой области спектра, а при комбинационном рассеянии – в видимой и ультрафиолетовой области спектра. Эти спектры состоят из отдельных линий и поэтому их называют линейчатыми.
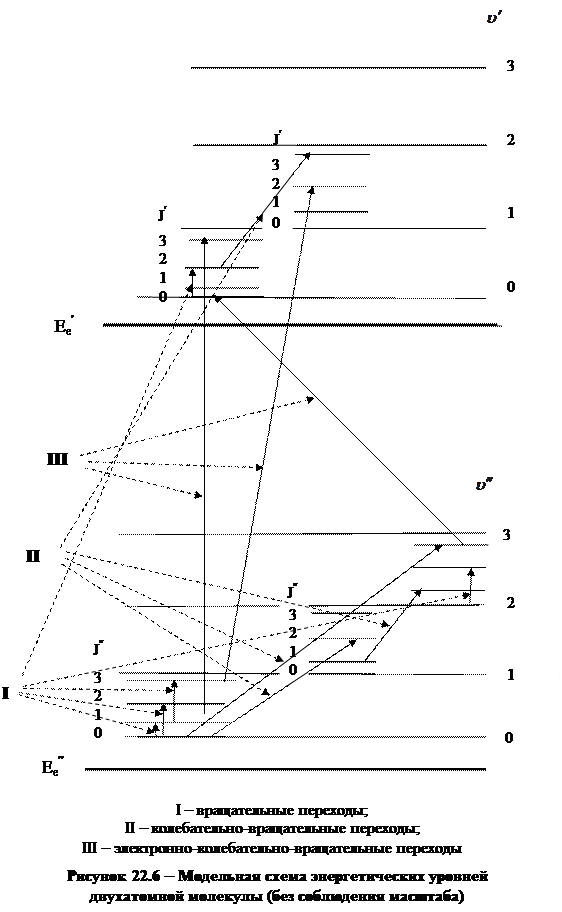
Квантовые переходы, объединенные на схеме в группу II, сопровождаются одновременным изменением колебательной и вращательной энергии молекулы, поэтому соответствующие им спектры называют вращательно-колебательными спектрами молекул. Частоты, соответствующие изменению вращательного движения молекулы, значительно (в 100 ÷ 1000) раз меньше частот излучения, сопровождающего изменение колебательного движения. В результате наложения колебательных и вращательных спектров линии колебательного спектра превращаются в полосы, каждая из которых содержит группы линий, соответствующие вращательному спектру. Так формируется линейчато-полосатая структура вращательно-колебательного спектра. Так как 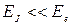 , то на спектр, соответствующий электронным переходам, вращение молекулы практически не влияет.
, то на спектр, соответствующий электронным переходам, вращение молекулы практически не влияет.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 5254; Нарушение авторских прав?; Мы поможем в написании вашей работы!