
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод интегрирования по частям
|
|
|
|
J Пример 22.1.
1) 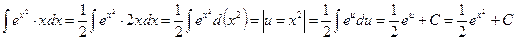 .
.
2)
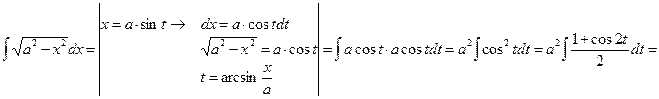
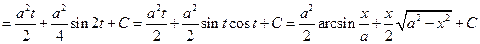 .
.
3) а) 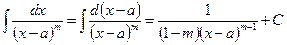
 .
.
б) 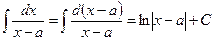 .
.
в) 
(доказательство формулы 8 таблицы интегралов лекции 21).
г) 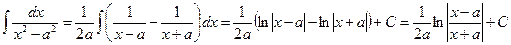
(доказательство формулы 12 таблицы интегралов лекции 21).
4) а) При 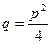
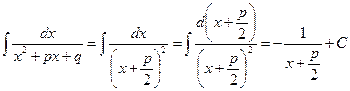 .
.
б) При  ,
, 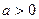 ,
,
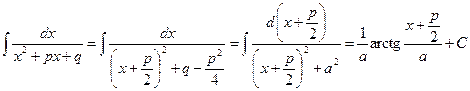 .
.
в) При 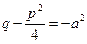 ,
, 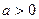 ,
,
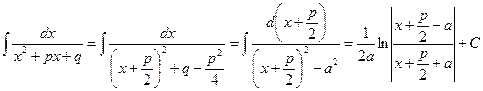 . (22.2)
. (22.2)
г) 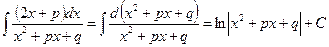 .
.
д) При 
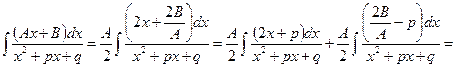
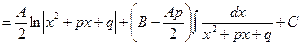 ,
,
где последний интеграл вычисляется по (22.2). J
J Пример 22.2. Вычислить заменой переменных интегралы
1) 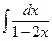 , 2)
, 2)  , 3)
, 3) 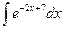 , 4)
, 4)  , 5)
, 5) 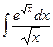 ,
,
6)  , 7)
, 7)  , 8)
, 8) 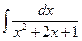 , 9)
, 9) 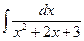 ,
,
10)  , 11)
, 11) 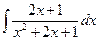 , 12)
, 12) 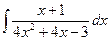 , 13)
, 13)  . J
. J
♦ Теорема 22.1 (формула интегрирования по частям). Пусть 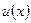 и
и 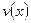 – непрерывно дифференцируемые функции. Тогда
– непрерывно дифференцируемые функции. Тогда
 . (22.3)
. (22.3)
Доказательство. Имеем 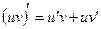 , следовательно
, следовательно  и после интегрирования получаем:
и после интегрирования получаем: 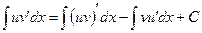 . Окончательно:
. Окончательно:
 .
.
Постоянную C обычно опускают, так как в правой части формулы интегрирования по частям стоит неопределённый интеграл. ■
Интеграл 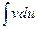 может оказаться более простым, чем
может оказаться более простым, чем 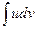 . Большую часть интегралов, вычисляемых методом интегрирования по частям, можно разбить на 3 группы:
. Большую часть интегралов, вычисляемых методом интегрирования по частям, можно разбить на 3 группы:
1) 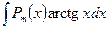 ,
, 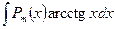 ,
, 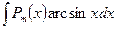 ,
,  ,
,  , где
, где 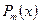 – многочлен степени m. При вычислении интегралов этой группы, необходимо за
– многочлен степени m. При вычислении интегралов этой группы, необходимо за 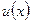 принять
принять  (обратную тригонометрическую функцию или логарифм) и положить
(обратную тригонометрическую функцию или логарифм) и положить 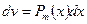 .
.
2) 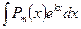 ,
, 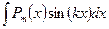 ,
, 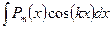 , где
, где 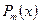 – многочлен степени m. При вычислении интегралов этой группы, необходимо принять
– многочлен степени m. При вычислении интегралов этой группы, необходимо принять 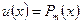 ,
, 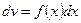 . Необходимо применить интегрирование по частям m раз.
. Необходимо применить интегрирование по частям m раз.
3) 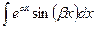 ,
, 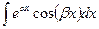 . Здесь необходимо применить двукратное интегрирование по частям, после чего искомый интеграл выражается сам через себя и находится из получающегося линейного уравнения 1‑го порядка.
. Здесь необходимо применить двукратное интегрирование по частям, после чего искомый интеграл выражается сам через себя и находится из получающегося линейного уравнения 1‑го порядка.
J Пример 22.3. 1)  .
.
2)  .
.
3) 
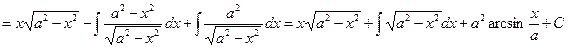 ,
,
откуда 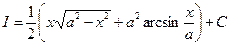 . J
. J
J Пример 22.4. 1)
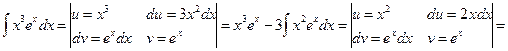
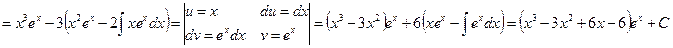 .
.
2)  ,
, 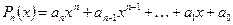 – алгебраический многочлен. Применяем n -кратное интегрирование по частям. Так как характер первообразной легко угадывается, то эти интегралы можно вычислять методом неопределённых коэффициентов.
– алгебраический многочлен. Применяем n -кратное интегрирование по частям. Так как характер первообразной легко угадывается, то эти интегралы можно вычислять методом неопределённых коэффициентов.
Например, для  первообразная имеет вид:
первообразная имеет вид:
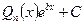 , где
, где 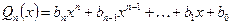 .
.
Коэффициенты находим из условия


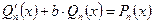 .
.
3) 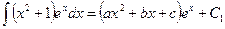 ;
; 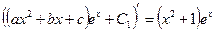 ,
,
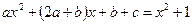 ,
, 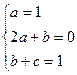
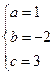
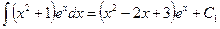 .
.
J
J Пример 22.5. 1)
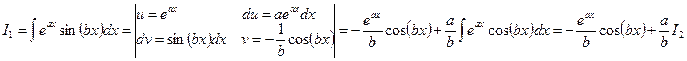 .
.
Здесь можно было поступить наоборот и принять 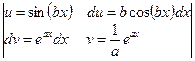 . Далее имеем:
. Далее имеем:
 ,
,
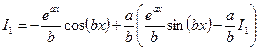 ,
, 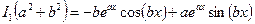 ,
,
 .
.
2) Тем же самым способом можно получить, что
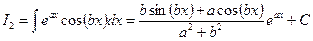 ,
,
а можно найти 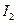 по связи с
по связи с 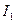 . J
. J
22.3. Некоторые рекуррентные [1] формулы.
1) Метод интегрирования по частям для интеграла 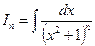 ,
, 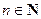 ,
, 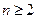 приводит к рекуррентному выражению
приводит к рекуррентному выражению  , где
, где
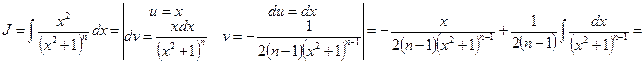
 ,
,
и окончательно:
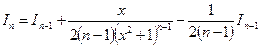 ,
,
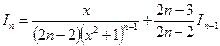 .
.
Используя это выражение, можем понизить индекс на единицу, двойку и т.д., что приводит к цепочке формул:
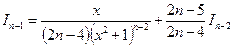 ,
,
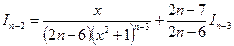 ,
, 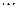 ,
,
приводящей к 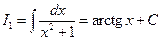 .
.
J Пример 22.6. 1) 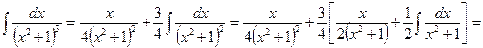
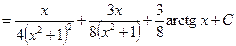 . J
. J
2) Рассмотрим также интеграл  :
:
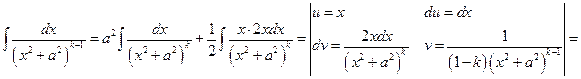


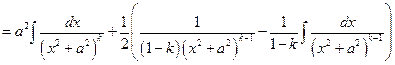 ,
,
то есть
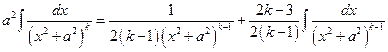 .
.
Применяя тот же процесс, приводящий к понижению на единицу показателя степени в знаменателе подынтегральной дроби, придём к 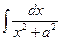 .
.
Таким образом, при 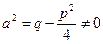 и
и  интеграл
интеграл 
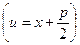 берётся в элементарных функциях.
берётся в элементарных функциях.
[1] От лат. recurrens – возвращающийся.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 362; Нарушение авторских прав?; Мы поможем в написании вашей работы!