Лекции 20, 21. Нелинейное преобразование случайных сигналов. Статистическая линеаризация нелинейных элементов

Вопросы для обсуждения на семинарском занятии

Темы рефератов

1. Социальная помощь красноармейцам в 20-е годы.

2. Институт шефства как социальная форма общественной помощи в советский период.

3. Система благотворительности в 90-е годы в Российской федерации.

4. Система учреждений социальной защиты на рубеже XX—XXI веков.

1. Покажите, какие мероприятия разворачиваются в первые годы Советской власти в области социальной поддержки.

2. Какие меры предпринимаются НКСО, чтобы ликвидировать проявления социальной патологии в 20-е годы?

3. Как строится работа с инвалидами в Советской России?

4. Покажите особенности социального обеспечения в 1941-1945 годах в СССР.

5. Дайте характеристику основных тенденций в области социального обеспечения в 60 — 70-е годы.

6. Покажите особенность формирования системы социальной защиты населения в 90-е годы.

7. Дайте характеристику основных тенденций социальной защиты населения РФ на рубеже веков.

Литература

1. Антология социальной работы в России / Сост. Фирсов М.В. М., 1994- 1995.

2. Бадя Л.В., Демина Л.И., Егошина В.Н. и др. Исторический опыт социальной работы в России. М., 1994.

3. Фирсов М.В. Методологические проблемы институционализации социальной работы. М., 2000.

4. Фирсов М.В. Социальная работа в России: теория, история, общественная практика. М., 1996.

5. Холостова Е.И. Генезис социальной работы в России. М., 1994.

6. Энциклопедия социальной работы: В 3 т. Т. 1. М.,
1994.

План.

1.Постановка задачи.

2.Прохождение случайного сигнала через нелинейный безынерционный элемент с зоной насыщения.

3.Плотность вероятности выходного сигнала.

4.Критерии статистической эквивалентности.

5.Расчет коэффицициентов статистической линеаризации

на основе первого критерия.

6. Расчет коэффицициентов статистической линеаризации

на основе второго критерия.

7.Примеры статистической линеаризации нелинейных элементов.

Нелинейные элементы в общем случае вызывают искажение входного преобразование Фурье от ординат дискретной корреляционной функции:

В нелинейных системах принцип суперпозиции неприменим, поэтому при одновременном воздействии на систему, например, полезного регулярного сигнала и случайной помехи из-за нелинейного преобразования этих сигналов помеха может значительно уменьшить эффект действия полезного сигнала.

Допустим, что на вход нелинейного элемента поступает случайный сигнал

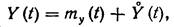
(20.1)

где m_y(t) — математическое ожидание (среднее значение) входного воздействия;

Y⁰(t) — центрированная случайная составляющая входного воздействия.

Предполагая, что случайный процесс является стационарным, т. е. m_y(t)=m_y=const, рассмотрим, как будет искажаться входной случайный сигнал при прохожденииего, например, через нелинейный безынерционный элемент с зоной насыщения (рис. 20.1).

При малом уровне помех, когда входное воздействие не выходит за пределы линейного рабочего участка, имеющего угол наклона а, выходной сигнал равен

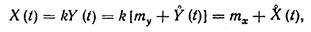
(20.2)

где k=tga — коффициент усиления элемента;

m_x=km_y — математическое ожидание сигнала на выходе элемента;

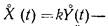центрированная случайная составляющая сигналана выходе элемента.

В этом случае среднее значение выходного сигнала т^ пропорционально среднему значению входного сигнала т.

С ростом уровня помех, когда входное воздействие выходит за пределы линейного участка, среднее значение выходного сигнала уменьшается и при очень большом уровне помех оказывается близким к нулю.

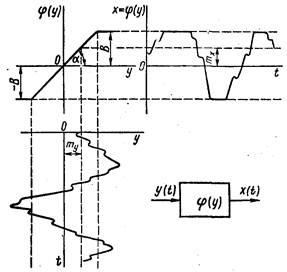
Рис. 20.1

Таким образом, увеличение уровня помех, определяемого дисперсией случайного входного сигнала, уменьшает полезный сигнал на выходе нелинейного элемента, что эквивалентно уменьшению коэффициента преобразования нелинейного элемента.

Одновременно с этим выходной сигнал обогащается как высокочастотными, так и низкочастотными гармониками, т. е. происходит изме­нение спектрального состава выходного случайного процесса по сравнению со спектральным составом входного случайного процесса.

Допустим, например, что на нелинейный элемент типа насыщения поступает случайный сигнал, среднее значение которого т_y, a плотность вероятности w(у) соответствует нормальному закону распределения (рис. 20.2),

Линейный участок характеристики в пределах ± b не оказывает влияния на форму кривой плотности вероятности, т.е. w(x) = w(y) при |у| < b.

Выходной сигнал нелинейного элемента не может превышать уровня насыщения В, поэтому вероятность появления сигнала, большего по абсолютной величине, чем В, равна нулю, т. е. w(x) = 0 при |у|>b.

Всем значениям входного сигнала у>b (у < -b) будет соответствовать значение выходного сигнала х = В (х=-В), поэтому вероятность получения величины В(-В) на выходе нелинейного элемента сильно возрастает и становится равной величине заштрихованной площади под участком кривой плотности вероятности входного сигнала, лежащей в пределах от у=b до у=∞. Это выразится в том, что плотность вероятности выходного сигнала w(x) в точках у=±b будет представлять собой d -функции, т. е. импульсы бесконечно большой величины и бесконечно малой ширины, площадь S которых равна заштрихованной площади под соответствующим (правым или левым) участком кривой плотности вероятности входного сигнала.

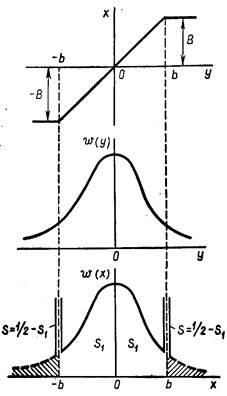
Рис. 20.2

Таким образом, выражение для плотности вероятности выходного сигнала может быть записано следующим образом:

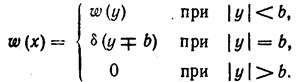
(20.3)

Общая площадь под кривой плотности вероятности выходного сигнала, естественно, остается равной единице, т. е.

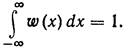
(20.4)

Исследование нелинейных систем, находящихся под воздействием случайных процессов, значительно сложнее, чем линейных систем.

Общих точных методов исследования подобных систем нет, и для изучения систем в этом случае обычно используют приближенные методы.

Дата добавления: 2014-01-04