Статистическая линеаризация нелинейных элементов

Наибольшее распространение в практике расчета нелинейных систем при случайных воздействиях получил приближенный метод, называемый методом статистической линеаризации. Этот метод был разработан в 1954 г. одновременно И. Е. Казаковым в СССР и Р. Бутоном в США.

Идея метода основана на приближенной замене нелинейных преобразований процессов, происходящих в системе, статистически эквивалентными им линейными преобразованиями, при этом нелинейный элемент заменяется статистически эквивалентным линейным элементом. В результате такой замены система в целом линеаризуется и дляее исследования можно применять аппарат линейной теории.

Возможны различные критерии статистической эквивалентности, которые могут быть положены в основу метода статистической линеаризации. В тех случаях, когда линеаризуют безынерционный нелинейный элемент, у которого нелинейная зависимость между входным y(t) и выходным x(t) сигналами имеет вид

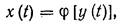
(20.5)

где j — статическая характеристика нелинейного элемента, применяют следующие два критерия:

1. Критерий равенства математического ожидания и дисперсии случайного процесса на выходе нелинейного элемента и эквивалентного ему линейного элемента.

2. Критерий минимума математического ожидания квадрата разности случайных процессов на выходе нелинейного элемента и эквивалентного ему линейного элемента.

Познакомимся с этими критериями, ограничиваясь рассмотрением только однозначных нелинейных характеристик, которые могут быть либо нечетными, либо четными.

Напомним, что для нечетных и четных характеристик соответственно справедливы соотношения

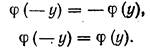
(20.6)

Случайные процессы на входе и выходе нелинейного элемента могут быть представлены следующим образом:

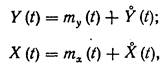
(20.7)

где т_y(t), m_x(t) — математические ожидания входного и выходного сигналов соответственно, включающие медленно меняющиеся регулярные составляющие; Y^o(t), X^o(t) — центрированные случайные составляющие процессов на входе и выходе нелинейного элемента соответственно.

Заметим, что для четных нелинейных характеристик, обладающих выпрямляющими свойствами, математическое ожидание m_x(t) отлично от нуля даже при m_y(t)=0.

В общем случае для однозначной нелинейной функции j(t) произвольного вида сигнал на выходе эквивалентного линеаризованного элемента

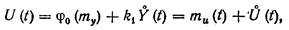
(20.8)

где j₀(m_y) — математическое ожидание нелинейной функции j(у);

k₁ — эквивалентный статистический коэффициент усиления по случайной центрированной составляющей.

Таким образом, в общем случае нелинейный безынерционный элемент (рис. 20.3, а) заменяют двумя безынерционными элементами: нелинейным по математическому ожиданию и линейным по случайной центрированной составляющей (рис.20.3, б).

Рис. 20.3

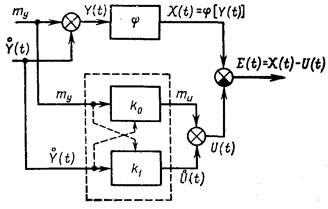
Рис. 20.4

В частном случае, когда нелинейный безынерционный элемент имеет нечетную характеристику, функция j₀ может быть представлена в виде

(20.9)

где k₀ — эквивалентный статистический коэффициент усиления нелинейного элемента по математическому ожиданию (по средней составляющей).

В этом случае нелинейный элемент можно эквивалентно заменить двумя линейными элементами с коэффициентами усиления k₀ и k₁ (рис. 20.4). Численные значения этих коэффициентов при заданной нелинейной зависимости j определяются значениями математического ожидания и дисперсии случайного сигнала на входе нелинейного элемента.

Покажем сначала, как находят коэффициенты j₀, k₀, k₁ в случае статистической линеаризации, основанной на первом критерии статистической эквивалентности, состоящем в выполнении равенства математического ожидания и дисперсии случайного процесса на выходе нелинейного элемента и эквивалентного ему линейного элемента, т. е. когда

(20.10)

Принимая во внимание (195), получаем

(20.11)

Для нечетных нелинейностей, учитывая (196), получим

(20.12)

Чтобы найти статистически эквивалентный коэффициент k₁, перепишем (198) следующим образом:

(20.13)

откуда

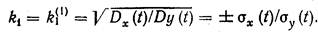
(20.14)

Обозначение показывает, что коэффициент k₁ найден по первому критерию эквивалентности.

Статистические коэффициенты j₀, k₀ и можно также выразить через нелинейную зависимость j и плотность вероятности w(y) случайного сигнала Y(t) на входе нелинейного элемента:

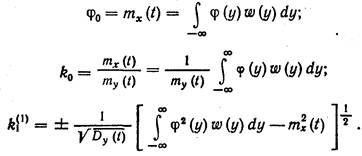
(20.15)   (20.16)   (20.17)

Знаки в (201) и (204) следует выбирать такими, чтобы знаки X(t) и U(t) совпадали.

Второй критерий статистической эквивалентности требует выполнения условия минимума математического ожидания квадрата разности процессов на выходе нелинейного элемента и эквивалентного линейного элемента, т. е.

(20.18)

Подставляя в (205) значения X(t) и U (t), определяемые по (194) и (195), получим

(20.19)

После выполнения операции возведения в квадрат и вычисления математического ожидания имеем

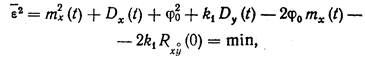
(20.20)

где m_x(t) — математическое ожидание случайного процесса на выходе нелинейного элемента;

- дисперсия центрированного случайного процесса на входе и выходе нелинейного элемента соответственно;

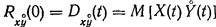- математическое ожидание (среднее значение) произведения двух случайных функций X(t) и Y(t), равное начальному значению взаимной корреляционной функции R_xy о(0).

При заданных значениях m_x(t), D_y(t), D_x(t), R_xyo(0) величина e² является функцией параметров j₀ и k₁.

Значения j₀ и k₁, при которых выполняется (205), найдем, если приравняем нулю частные производные функции e² по параметрам j₀ и k₁. Имеем

(20.21)

откуда

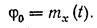
(20.22)

В случае нечетной нелинейной характеристики j, учитывая (196) получаем следующее выражение для коэффициента k_:

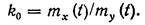
(20.23)

Значениекоэффициента k₁ находимиз

(20.24)

откуда

(20.25)

Обозначение k₁⁽²⁾ показывает, что коэффициент k₁, найден по второму критерию эквивалентности.

Статистический коэффициент k₁⁽²⁾ можно выразить также через плотность вероятности w(у) входного случайного сигнала Y(t) и нелинейную зависимость j, т. е.

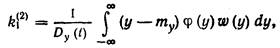
(20.26)

где

(20.27)

Обычно значение коэффициента k₁⁽¹⁾, определенное из первого критерия по (201), является несколько завышенным, а k₁⁽²⁾, определенное из второго критерия по (209), — несколько заниженным, поэтому при расчетах рекомендуется брать их среднеарифметическое значение, т. е.

(20.28)

Пример 9. На входе нелинейного элемента, имеющего статическую квадратичную зависимость x=j(y)=ky² между входным и выходным сигналом, действует случайный сигнал Y(t) = т_у + Y⁰(t), имеющий нормальный закон распределения. Определить эквивалентные статистические коэффициенты усиления j₀ и k₁⁽²⁾.

1. Поскольку характеристика нелинейного элемента является четной, то в соответствии с (202) функция j₀ равна

(20.29)

2. На основании (9.217), дифференцируя полученное выражение для j₀, определяем коэффициент k₁⁽²⁾:

(20.30)

Рис. 20.5

Пример 10. На входе нелинейного элемента типа идеального реле с характеристикой

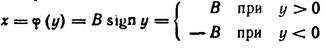
(20.31)

действует случайный сигнал Y(t)=m_y(t)+Y⁰(t), имеющий нормальный закон распределения. Определить эквивалентные статистические коэффициенты усиления нелинейного элемента.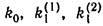

1. Определяем эквивалентный статистический коэффициент усиления по математическому ожиданию k₀ по (214), т. е.

(20.32)

Вводя обозначение

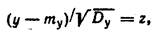
(20.33)

получаем

(20.34)

где

(20.35)

2. Определяем эвкивалентный статистический коэффициент усиления k₁⁽¹⁾ по случайной составляющей по (9.204):

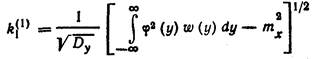
(20.36)

Учитывая, что

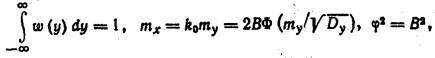
(20.37)

получаем

(20.38)

3. Определяем эквивалентный статистический коэффициент усиления случайной составляющей по (21 б):

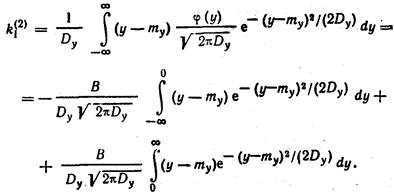
(20.39)

Учитывая (218), получаем

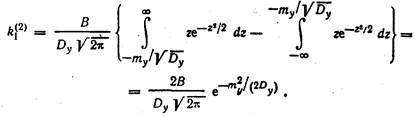
(20.40)

Из (219), (220) и (221) видно, что при нормальном законе распределения коэффициенты k₀, k₁⁽¹⁾ и k₁⁽²⁾ выражаются через функцию Крампа (нормированный интеграл плотности вероятности)

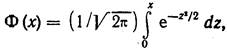
(20.41)

Для вычисления коэффициентов статистической линеаризации достаточно знать математическое ожидание т_y и дисперсию D_y случайного процесса на входе нелинейного элемента и значения функции Крампа для аргументов, определяемых через т_y и D_y.

Построенные по (219), (220) и (221) графики коэффициентов статистической линеаризации идеального реле приведены на рис. 20.5, б, в. Из этих графиков видно, что релейный элемент по отношению к среднему значению входного сигнала т_y ведет себя как линейное звено, коэффициент усиления которого k₀ зависит от величины

Таким образом, случайная составляющая входного сигнала создает эффект линеаризации нелинейного элемента для регулярной составляющей (среднего значения) сигнала. Метод статистической линеаризации формально похож на метод вибрационной линеаризации нелинейного элемента колебаниями высокой частоты постоянной амплитуды.

В свою очередь регулярная составляющая входного сигнала оказывает влияние на прохождение случайной составляющей. Так, например, для рассмотренного нелинейного элемента типа идеального реле передача случайной составляющей ослабляется за счет насыщения нелинейного элемента регулярной составляющей сигнала, поскольку коэффициенты k₁⁽¹⁾ и k₁⁽²⁾ уменьшаются с ростом т_y.

Ограничения в использовании метода статистической линеаризации обусловлены требованиями нормального закона распределения случайного процесса на входе нелинейного элемента, что выполняется достаточно хорошо, если линейная часть системы будет обладать свойствами низкочастотного фильтра.

Для нормального закона распределения значения коэффициентов k₀, k₁⁽¹⁾ и k₁⁽²⁾ для различных типовых нелинейных элементов заранее определены по (213), (214), (215), (216) и приведены в виде графиков зависимости этих коэффициентов от математического ожидания m_у и дисперсии D_y входного случайного сигнала. Использование этих графиков значительно упрощает расчет конкретных систем автоматического управления методом статистической линеаризации.

Метод статистической линеаризации особенно эффективен при анализе стационарного режима работы системы автоматического управления. В этом случае т_y=const, D_y=const и коэффициенты статистической линеаризации не зависят от времени. Линеаризованная система является при этом системой с постоянным параметрами и ее исследование может быть проведено сравнительно просто.

В нестационарном режиме, который может быть вызван, например, переходным процессом, нестационарностью воздействий или самой системы, коэффициенты статистической линеаризации изменяются во времени. Линеаризованная система оказывается при этом системой с переменными параметрами и ее исследование усложняется. Исследования системы в этом случае могут производиться с помощью аналоговых или цифровых вычислительных машин.

Дата добавления: 2014-01-04