Метод Эйлера — разные подходы к построению

Лекция 22. ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Учитывая ключевую позицию, которую занимает метод Эйлера в теории численных методов ОДУ, рассмотрим несколько способов его вывода. При этом будем считать, что вычисления проводятся с расчетным шагом 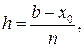расчетными точками (узлами) служат точки х_i = х ₀ + ih (i = 0,1,.,., n) промежутка [ х ₀, b ] и целью является построение таблицы

x	x 0		x 1	…	xn=b
y	y 0		y 1	…	yn=y (b)

приближенных значений y_i решения у = у (х) задачи

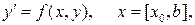(22.1)

y (x ₀) = y ₀ (22.2)

в расчетных точках x_i.

Геометрический способ. Пользуясь тем, что в точке x ₀ известно и значение решения y (x ₀) = y ₀ (согласно (22.2)), и значение его производной (согласно (22.1)), можно записать уравнение касательной к графику искомой функции у = у (х) в точке (х ₀; у ₀):

(22.3)

При достаточно малом шаге h ордината

(22.4)

этой касательной, полученная подстановкой в правую часть (22.3) значения х ₁ = х ₀ + h по теореме о непрерывной зависимости решений от начальных данных должна мало отличаться от y (x ₁) ординаты решения y (x) задачи (22.1)-(22.2). Следовательно, точка (x ₁ ,y ₁) может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую

которая уже приближенно отражает поведение касательной к решению у = у (х) в точке. Подставляя сюда + h), получим приближение значения у (x ₂) значением

и т.д. В итоге этого процесса, определяемого формулой

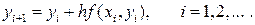(22.5)

и называемого методом Эйлера, график решения у = у (х) данной задачи Коши (22.1) – (22.2) приближенно представляется ломаной, составленной из отрезков приближенных касательных, откуда происходит другое название метода (22.5) — метод ломаных.

Применение формулы Тейлора. Описываемый здесь способ вывода метода Эйлера тесно связан с предыдущим. Линеаризуя решение в окрестности начальной точки по формуле Тейлора, имеем

Отсюда при x = x ₁ получаем

Сравнивая это равенство с формулой (22.4), видим, что ее остаточный член имеет вид

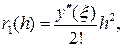(22.6)

где x — некоторая точка интервала (x ₀, х ₁).

Остаточный член (22.6) характеризует локальную (или, иначе, шаговую) ошибку метода Эйлера, т.е. ошибку, совершаемую на одном шаге. Очевидно, что от шага к шагу, т.е. при многократном применении формулы (22.5), возможно накопление ошибок. За п шагов, т.е. в точке b, образуется глобальная ошибка изучение такой ошибки будет проведено позже. Сейчас же анонсируем один важный хотя бы для терминологии факт: порядок глобальной ошибки (относительно шага h) на единицу ниже, чем порядок локальной ошибки, а порядком глобальной ошибки и определяется порядок соответствующего численного процесса решения задачи Коши. Таким образом, локальная ошибка метода Эйлера, согласно (22.6), есть O (h²), глобальная — O (h), т.е. метод Эйлера относится к методам первого порядка.

Квадратурный способ. Н ачальную задачу для ОДУ (22.1)-(22.2) можно заменить эквивалентным интегральным уравнением

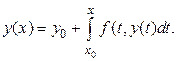(22.7)

При x = x ₁ из него получится равенство

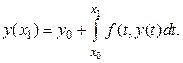(22.8)

Применение к интегралу в правой части равенства простейшей (одноточечной) формулы левых прямоугольников дает приближенную формулу

правая часть которой, очевидно, совпадает с выражением (22.4) для подсчета значения y ₁. Для получения формулы (22.5) следует применить метод левых прямоугольников к интегралу

(22.9)

которая получается из формулы (22.8) заменой точки (x ₀, y ₀) точкой (x_i, y_i), а точки (x ₁, y ₁) точкой (x_{i +1}, y_{i +1}).

Дата добавления: 2014-01-04