
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тригонометрический ряд
|
|
|
|
Рассмотрим теперь бесконечную сумму произведений тригонометрических функций с некоторыми постоянными числами, т.е. перейдем в (2) к пределу при  .
.
| Опр. | Тригонометрическим рядом называется функциональный ряд вида
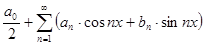 где действительные числа
где действительные числа 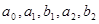 - называются коэффициентами этого ряда. - называются коэффициентами этого ряда.
|
Если тригонометрический ряд сходится на отрезке 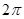 , в силу переодичности тригонометрических функций, он сходится на всей числовой оси, и его сумма
, в силу переодичности тригонометрических функций, он сходится на всей числовой оси, и его сумма 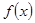 является переодической функцией с периодом
является переодической функцией с периодом 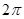 :
:
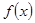 =
= 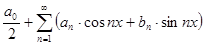 (3)
(3)
Соотношение (3) можно трактовать также как разложение функции 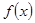 в тригонометрический ряд. В связи с этим напрашивается вопрос, нельзя ли любую
в тригонометрический ряд. В связи с этим напрашивается вопрос, нельзя ли любую 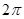 переодическую функцию представить в виде ряда простейших гармоник. При этом, очевидно, должны быть решены два вопроса: 1) каким требованиям должна удовлетворять
переодическую функцию представить в виде ряда простейших гармоник. При этом, очевидно, должны быть решены два вопроса: 1) каким требованиям должна удовлетворять 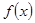 чтобы она была суммой некоторого тригонометрического ряда 2) и как построить такой ряд, т.е. как вычислить значения его коэффициентов. Ответим сначала на второй вопрос.
чтобы она была суммой некоторого тригонометрического ряда 2) и как построить такой ряд, т.е. как вычислить значения его коэффициентов. Ответим сначала на второй вопрос.
| Теорема | Если функциональный ряд
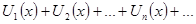 (4)
равномерно сходится на (4)
равномерно сходится на 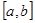 , то после умножения каждого его члена на непрерывную и ограниченную на этом отрезке функцию , то после умножения каждого его члена на непрерывную и ограниченную на этом отрезке функцию 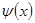 вновь полученный ряд вновь полученный ряд
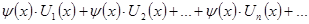 (5)
также равномерно сходятся на этом отрезке. (5)
также равномерно сходятся на этом отрезке.
|
Доказательство:
Т.к. 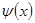 - непрерывна и ограничена на
- непрерывна и ограничена на 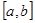 , то
, то 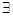 число
число 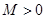 , что для всех
, что для всех 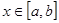 имеет место оценка
имеет место оценка 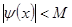 . (6)
. (6)
По критерию Коши равномерной сходимости ряда имеем:
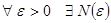 , такой, что для
, такой, что для 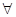
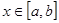 ,
, 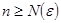 и
и 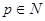 :
:
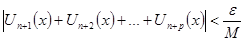 . (7)
. (7)
Тогда, использую (6) и (7): 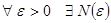 , такой, что
, такой, что 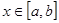 ,
, 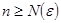 и
и 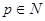 :
:
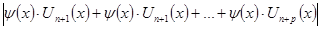 =
=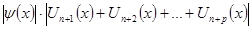 <
<
< 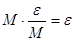 .
.
Доказанная теорема и лемма об ортогональности тригонометрических функций позволяет построить тригонометрический ряд для заданной функции и доказать его единственность.
| Теорема | Если функция 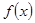 является суммой равномерно сходящегося тригонометрического ряда (3), то это разложение единственно, причем коэффициенты ряда вычисляются по формулам: является суммой равномерно сходящегося тригонометрического ряда (3), то это разложение единственно, причем коэффициенты ряда вычисляются по формулам:
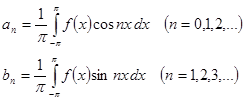 (8) (8)
|
Доказательство:
Пусть тригонометрический ряд (3) сходится на 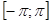 и его сумма равна
и его сумма равна 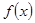 , причем функция
, причем функция 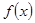 интегрируема на этом отрезке. Тогда на основании свойства
интегрируема на этом отрезке. Тогда на основании свойства  функциональных рядов, этот ряд можно проинтегрировать по
функциональных рядов, этот ряд можно проинтегрировать по 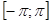 , в результате чего получим:
, в результате чего получим:
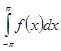 =
=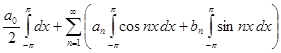 =
=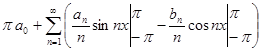 =
=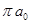
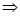
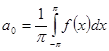
Умножив ряд (3) на непрерывную и ограниченную функцию 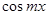
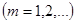 , получим ряд
, получим ряд
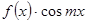 =
= 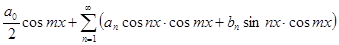 ,
,
который, согласно предыдущей теореме, также равномерно сходится на 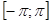 . Проинтегрируем этот ряд по
. Проинтегрируем этот ряд по 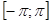 .
.
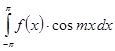 =
=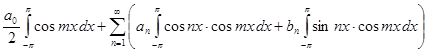 =
=
=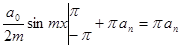 .
.
Т.е. 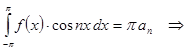
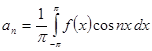 .
.
Аналогично получаем, что 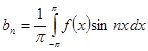 .
.
Необходимое условие разложения функции 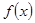 в тригонометрический ряд является существование интегралов (8).
в тригонометрический ряд является существование интегралов (8).
| Опр. | Тригонометрический ряд, коэффициенты которого определяются по формулам (8), называется рядом Фурье, а его коэффициенты – коэффициентами Фурье. |
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 764; Нарушение авторских прав?; Мы поможем в написании вашей работы!