Основные свойства дивергенции

- это дифференциальная характеристика поля; является скалярной величиной; в каждой точке 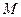поля 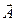показывает наличие источников или стоков поля:

если 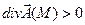, то в т. 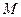есть источник поля 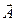; 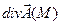численно равна мощности источника;

если , то в т. 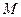есть сток поля 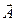; 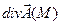численно равна мощности стока;

если 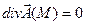, то в т. 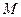нет ни источника, ни стока поля .

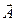вычисляется по формуле:

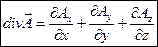
Доказательство:

Воспользуемся формулой Остроградского-Гаусса для :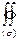

Þ

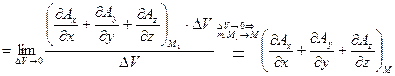, что и требовалось доказать.

Теорему Остроградского-Гаусса можно записать в векторной форме:

,

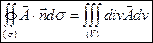то есть

Поток вектора 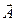изнутри замкнутой поверхности 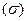равен тройному интегралу от дивергенции по объему, ограниченному этой поверхностью.

Линейность дивергенции:

.

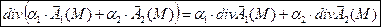Следует из линейности операций сложения векторов и дифференцирования.

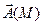Дивергенция произведения скалярного поля на векторное поле вычисляется по формуле:

.

Доказательство:

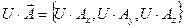Þ

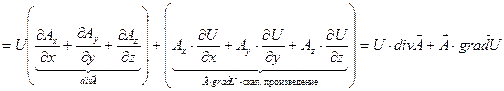, что и требовалось показать.

Примеры:

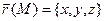- поле радиус-вектора т. .

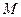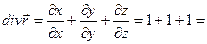
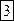, то есть каждая точка этого поля является источником постоянной мощности, равной 3.

,

;

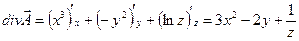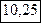
По рассмотренному примеру можно заметить, что

Любое векторное поле 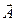сопровождает скалярное поле его дивергенций.

Дата добавления: 2014-01-04