Векторный дифференциальный оператор Гамильтона. Ротор векторного поля

Условимся, что обозначение производных по переменным x, y, z можно формально рассматривать как произведение символов дифференцирования 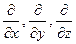и дифференцируемой функции:

.

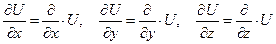При этом считается, что символ дифференцирования срабатывает тогда и только тогда, когда дифференцируемая функция стоит справа от него, т.е.:

.

При таком представлении символы 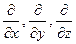называются операторами дифференцирования. Умножение их на функцию соответствует операции дифференцирования.

Введем вектор, координатами которого являются операторы дифференцирования :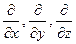

-

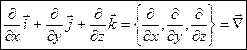дифференциальный оператор Гамильтона или оператор “набла”.

Здесь - это орты координатных осей .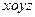

Дата добавления: 2014-01-04