Пример 4. Вычислить интеграл: , если

Вычислить интеграл: 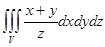, если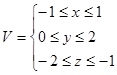

Решение:

Запишем данный интеграл как повторный:

.

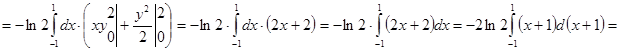
Основные свойства трехкратного интеграла.

Если область разбить на две области и плоскостью, параллельной какой-либо из плоскостей координат, то трехкратный интеграл по области равен сумме трехкратных интегралов по областям и . (При любом разбиении области на конечное число областей плоскостями, параллельными координатным плоскостям, имеет место равенство ).

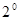(Теорема об оценке трехкратного интеграла)

Если и 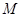, соответственно, наименьшее и наибольшее значение функции 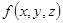в области , то имеет место неравенство:

Где есть объем данной области, а - трехкратный интеграл от функции 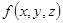по области .

(Теорема о среднем)

Трехкратный интеграл от непрерывной функции 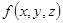по области равен произведению его объема на значение функции в некоторой точке области , то есть

Замена переменных в тройном интеграле.

Пусть функции

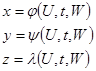
Взаимно однозначно отображают область в декартовых координатах 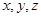на область в криволинейных координатах 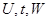. Пусть элемент объема области переходит в элемент 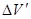области и пусть

.

Тогда

Аналогично тому, как это имело место в двойном интеграле

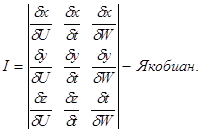
Тройной интеграл в цилиндрических координатах.

Декартовые координаты точки 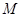пространства связаны с ее цилиндрическими координатами следующими соотношениями:

, .

Таким образом в цилиндрических координатах первые две координаты есть не что иное как полярные координаты точки (точка проекция точки 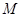на плоскость 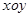). Третья координата является аппликатой точки .

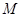Переход 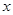цилиндрическим координатам в тройном интеграле целесообразен, очевидно, в тех случаях, когда область ограничена цилиндрической поверхностью с образующими, параллельными оси , а направляющей цилиндрической поверхностью является любая кривая, уравнения которой достаточно просто выглядит в полярных координатах.

Найдем Якобиан:

=

Итак,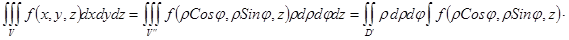

Определив пределы внутреннего интеграла по 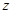и представив в виде двукратного интеграла, получим

.

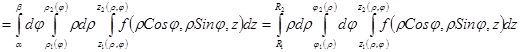Тройной интеграл в сферических координатах.

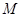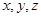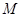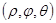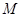Если точка в пространстве имеет прямоугольные координаты , то сферическими координатами точки называют тройку чисел , где -расстояние от точки до начала координат ;

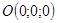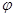- угол между лучом 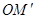(точка - проекция точки 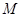на плоскость 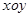) и осью ;

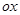- угол между положительным направлением оси 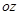и лучом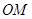

Связь между декартовыми и сферическими координатами определяются соотношениями.

Дата добавления: 2014-01-04