Доказать, что всякая сходящаяся последовательность является фундаментальной.

Доказательство. Пусть (х_n) – сходящаяся последовательность точек произвольного метрического пространства, 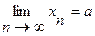и пусть d>0. Найдется такое N, что для всех n>N выполняется неравенство r(x_n, а)< d/2. А тогда по аксиоме треугольника для любых для любых n>N и m>N r(x_n, x_m)£ r(x_n, а)+ r(x_m, а) < d/2+d/2=d, ч.т.д.

Примеры 28.8.

Докажите, что если подмножество А метрического пространства М, рассматриваемое как самостоятельное метрическое пространство (с метрикой, заимствованной из М), является полным пространством, то А – замкнутое множество.

Доказательство. Рассмотрим произвольную сходящуюся в метрическом пространстве М последовательность (х_n) точек из множества А. чтобы убедиться, что А – замкнутое пространство, достаточно показать, что ее предел х Î А.

Так как (х_n) сходится в пространстве М, то последовательность (х_n) является в метрике этого пространства фундаментальной. Но в М и А метрика одинаковая, поэтому (х_n) фундаментальная и в А. Так как А – полное пространство, то х_n ®уÎ А. Итак, х_n ®хÎ М и х_n ®уÎ А по одной и той же метрике. В силу единственности предела в метрическом пространстве М отсюда следует, что х=у и, следовательно, х действительно принадлежит А.

Банаховы и гильбертовы пространства

Полное линейное нормированное пространство называется банаховым.

Приведем некоторые примеры банаховых пространств.

Примеры 28.9.

Пространство IR банахово. Действительно, на вещественной числовой оси имеет место критерий Коши: для того чтобы последовательность (х_n)ÌIR была сходящейся, необходимо и достаточно, чтобы она была фундаментальной. Справедливость критерия Коши в IR означает, что вся вещественная ось IR заполнена точками – вещественными числами, на ней нет «дыр», т.е. что она полна.

Если бы мы ограничились только рациональными числами, это было бы не так. Например, последовательность десятичных приближений к 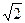с недостатком: х₁=1, х₂=1,4, х₃=1,41,… - фундаментальная, однако во множестве рациональных чисел она не является сходящейся (предел у нее есть и равен 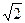, но это число иррациональное).

Примеры 28.10.

Пространство IR^m (m>1) также банахово, т.к. в IR^m тоже справедлив критерий Коши.

Примеры 28.11.

Пространство С([a;b]) является банаховым пространством. Пусть (х_n(t)) Ì С([a;b]). Справедлив следующий критерий Коши равномерной сходимости последовательности функций: для того чтобы (х_n(t)) сходилась в С([a;b]), т.е. равномерно на [a;b], необходимо и достаточно, чтобы для любого e>0 существовал номер N=N(e) такой, что при всех номерах n>N и любых натуральных р имело место неравенство 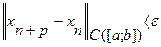, или иначе, 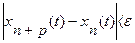для всех tÎ [a,b].

Полнота С([a;b]) отчетливо проступает также в следующей теореме: если последовательность непрерывных на [a;b] функций (х_n(t)) сходится равномерно на [a;b] к некоторой функции х(t), то х(t) непрерывна на [a;b].

Пусть Х – бесконечномерное банахово пространство. Последовательность (е_k)₁^¥ ÌХ называется базисом в Х, если любой элемент хÎХ может быть представлен в виде сходящегося ряда .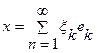

Пространство Н со скалярным произведением называется гильбертовым, если оно полно в норме, порожденной скалярным произведением.

Простейший пример гильбертова пространства дает евклидово пространство IR^m.

Углом между ненулевыми элементами х, у вещественного гильбертова пространства называется угол j, заключенный между 0 и p такой, что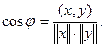

Элементы х,уÎН называют ортогональными и записывают х^у, если (х,у)=0. Множество zÎН таких, что (z,х)=0 для любого хÎМÌН, обозначается М^{^}.

Система элементов h₁,h₂,… ÎН называется ортогональной, если (h_i,h_j)=0 при i¹j, h_i¹0 и ортонормированной, если (h_i,h_j)=d_ij=.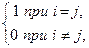

Система элементов х₁, х₂, …ÎН называется линейно независимой, если при любом натуральном n система х₁, х₂, … х_n линейно независима.

Пусть L – линейное многообразие в Н. Совокупность всех элементов из Н, ортогональных к L, называется ортогональным дополнением к L и обозначается L^{^}.

Теорема. L^{^} - подпространство в Н.

Доказательство. Докажем линейность L^{^}. Пусть, z₂ÎL^{^}, т.е. (z₁,y)=0, (z₂,y)=0 для любых уÎL. Тогда для любых скаляров l₁ и l₂ (l₁,z₁+l₂z₂,у)= l₁(z₁,у)+ l₂(z₂,у)=0 для любых уÎL, т.е. l₁,z₁+l₂z₂ ÎL^{^}.

Докажем замкнутость L^{^}. Пусть дана (z_n) Ì L^{^} и z_n®z, при n®¥. Для любых уÎL имеем (z_n,y)=0. Перейдем в этом равенстве к пределу при n®¥ по свойству непрерывности скалярного произведения, получим (z, y) = 0 для любого уÎL, т.е. zÎL^{^}. Теорема доказана.

Расстояние от точки х до подпространства L определяется формулой .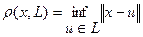

Существует единственный элемент уÎL, реализующий расстояние от точки х до подпространства L:

.

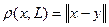Если , то х-у ^ L. Для любого хÎН справедливо разложение х=у+z, zÎL, причем это разложение единственное.

Пусть дана конечная или бесконечная последовательность линейно независимых векторов g₁, g₂,…,g_n,…

Покажем, как построить ортонормированную последовательность векторов е₁, е₂, …, е_n, … эквивалентную последовательности. В качестве первого вектора примем вектор 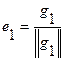, норма которого, очевидно, равна единице. Векторы е₁ и g₁ порождают одно и то же подпространство Е₁, одного измерения. Вектор g₂ мы построим в два приема. Сначала из вектора g₂ вычтем его проекцию на Е₁, получим вектор h₂=g₂–(g₂,е₁)е₁, который ортогонален подпространству Е₁, т.е. вектору е₁, и который не равен нулю, т.к. в противном случае вектор g₂ принадлежал бы Е₁, что противоречит линейной независимости векторов (1). Найдя h₂, положим 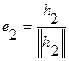. Векторы е₁, е₂ порождают то же подпространство двух измерений Е₂, что и векторы g₁, g₂.

Переходим к построению вектора е₃. Сначала из вектора g₃ вычтем его проекцию на Е₂; получаем вектор h₃=g₃ – (g₃,е₁) е₁– (g₃,е₂) е₂, отличный от нуля и ортогональный подпространству Е₂, т.е. ортогональный векторам е₁, е₂. Затем полагаем 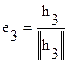. Подобным образом поступаем и далее. Если уже построены векторы е₁, е₂,…,е_n, то полагаем 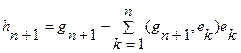, и затем .

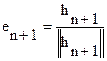Описанный прием носит название ортогонализации.

При решении многих вопросов относительно многообразия, порождаемого некоторой последовательностью векторов, предварительная ортогонализация этой последовательности может оказаться очень полезной.

Дата добавления: 2014-01-04