Вопрос № 4. Кинетика сушки

Сушка, как уже отмечалось, является сложным тепломассообменным процессом. Влага из влажного материала к поверхности раздела фаз перемещается за счет массопроводности, а от поверх­ности раздела фаз в ядро газового потока — за счет конвективной диффузии.

Диффузия влаги в материале происходит не только вследствие градиента влагосодержания материала, но и под действием темпе­ратурного градиента.

Аналитическое описание диффузии влаги в материале пред­ставляет достаточно сложную задачу. Процесс сушки протекает со скоростью, зависящей от формы связи влаги с материалом и меха­низма диффузии влаги в нем. Кинетика сушки характеризуется изменением во времени средней влажности материала или влаго­содержания.

Для определения скорости сушки опытным путем получают кривую сушки, а затем, дифференцируя ее, — кривую скорости сушки.

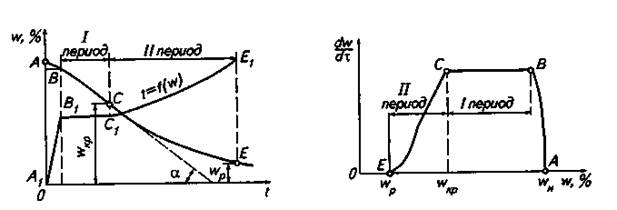
Зависимость между средней влажностью материала и продол­жительностью сушки изображается кривой сушки (рис. 1). На этом же рисунке приведена зависимость температуры материала от его влажности. Типичная кривая сушки состоит из нескольких участков, соответствующих различным периодам сушки. После периода прогрева материала до температуры сушки (участок АВ) наступает период постоянной скорости сушки (I период). В этот период температура материала принимает значение, равное тем­пературе мокрого термометра t _м (отрезок В₁С₁ на температурной кривой). В период постоянной скорости сушки теплота, подводи­мая к материалу, расходуется на испарение свободной влаги. Пе­риод постоянной скорости сушки изображается прямой линией с постоянным тангенсом угла наклона (отрезок ВС). Этот период продолжается до достижения первой критической влажности w _кр. Начиная с w _кр, наступает период падающей скорости. В этом пе­риоде снижение влажности материала выражается кривой СЕ. В период падающей скорости удаляется связанная влага и темпера­тура материала повышается по кривой С₁Е₁. В конце сушки влаж­ность материала асимптотически приближается к равновесной влажности w_p. При достижении равновесной влажности прекра­щается удаление влаги из материала. В этот момент температура материала достигает значения, равного температуре окружающего материал теплоносителя (точка Е₁). Однако для достижения рав­новесной влажности требуется значительное время. Скорость сушки представляет собой изменение влажности (влагосодержание) в единицу времени: dW/dτ (%/ч), или dx/dτ (с^-1).

Рис. 1. Кривая сушки Рис.2. Кривая скорости сушки

Скорость сушки для данной влажности (влагосодержания) ма­териала выражается тангенсом угла наклона касательной, прове­денной к точке кривой сушки, определяющей влажность или влагосодержание материала.

По данным о скорости сушки строится кривая скорости сушки (рис. 2). Горизонтальный отрезок ВС определяет скорость в первом периоде сушки, а отрезок СЕ — во втором.

В первом периоде сушки удаляется свободная влага и скорость сушки определяется сопротивлением массопереносу во внешне-диффузионной области, т. е. значением конвективного крэффициента массоотдачи. В точке С, соответствующей первой крити­ческой влажности w _Kp1, влажность на поверхности материала ста­новится равной гигроскопической. Со значения w_Kpl начинается удаление из материала связанной влаги и скорость процесса суш­ки снижается.

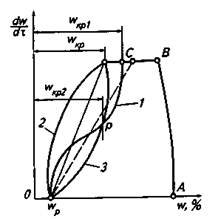
Отметим, что вид кривых скорости сушки во втором периоде может значительно отличаться от приведенного на рис. 2. Вто­рой период сушки в зависимости от форм связи влаги с материа­лом может сам складываться из нескольких периодов. Кривая 1(рис. 3) типична для капиллярно-пористых тел (например, сухарей), для которых верхний участок определяет скорость удаления капил­лярной влаги, а нижний, начиная с влажности, равной w_Kp2, — адсорбци­онной. Линии 2 и 3 соответствуют скоростям сушки, большей и мень­шей, чем те, которые подчиняются прямолинейному закону.

Рис. 3. Типичные кривые скорости сушки для капиллярно-пористых тел

Первая получается при сушке, например, тканей и других тонколистовых материалов или когда материал растрескивается во время сушки, вторая — при сушке, например, керамических материалов или когда на поверхности материала образуется корка, препятствующая диффузии влаги к поверхности раздела фаз.

Скорость сушки определяет один из важнейших технологичес­ких параметров сушки — ее интенсивность. Интенсивность испарения влаги из материала [кг/(м² · с)] определяется количеством удаляемой влаги в единицу времени с единицы площади поверх­ности высушиваемого материала: I= W/(Fτ).

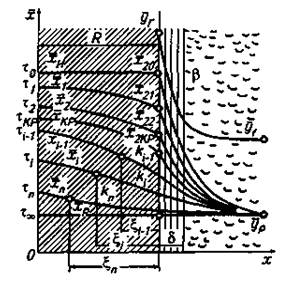
Схема диффузии влаги из твердого влажного материала изобра­жена на рис. 4.

Рис. 4. Модель массопереноса вещества в капиллярно-пористом теле

Влага внутри твердого влажного материала перемещается к поверхности за счет массопроводности (см. «Массопеоедача с твердой фазой»). От поверхности раздела фаз в ядро га­зового потока влага передается за счет конвективной диффузии. Перемещение вещества в капиллярно-пористых материалах может осуществляться одновременно под действием градиентов концентраций и температур. Последнее обстоятельство вызывает явление термодиффузии, которое особенно сильно проявляется при жестких режимах сушки, когда в материале образуются значи­тельные градиенты температур.

При р = cоnst массовый поток

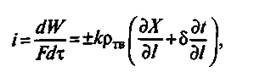(1)

где k - коэффициент массопроводности, м²/ч; ρ _тв — плотность абсолютно сухого материала кг/м³; X— влагосодержание материала, кг на 1 кг абсолютно сухого материала l —нормаль к изоконцентрационной поверхности; δ — коэффициент термовлагопроводности, К^-1; t-температура, К.

Первый член уравнения (1) характеризует перенос вещества под действием градиента концентраций, второй — под действием градиента температур.

Кинетические коэффициенты k и δ в этом уравнении являются функциями температуры и влажности тела, поэтому перенос влаги во влажном теле следует рассматривать совместно с распростране­нием теплоты в материале, которое описывается законом тепло­проводности Фурье

(2)

На основании приведенных уравнений массотеплопроводности и Лыковым получена система дифференциальных уравнений тепломассопереноса (при р = const) в капиллярно-пористом теле

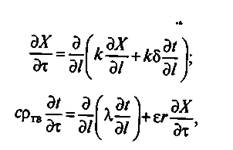(3)

где ε = dX_ф/dX— критерий фазового превращения — отношение локального бес­конечно малого изменения влагосодержания за счет фазового превращения (ис­парения или конденсации) к общему локальному изменению влагосодержания; r — теплота испарения, кДж/кг.

Коэффициенты λ, с, ε, r в этом уравнении являются перемен­ными величинами, зависящими от влажности и температуры тела.

Первое уравнение системы описывает скорость изменения вла­госодержания в твердом теле под действием градиентов влажности и температур.

Второе уравнение характеризует скорость изменения темпера­турного поля за счет теплопроводности и внутреннего испарения.

Дата добавления: 2014-01-04