Пример 2. Рассмотрим поток несжимаемой жидкости, имеющей постоянную плоскость

Рассмотрим поток несжимаемой жидкости, имеющей постоянную плоскость. Тогда вектор скорости жидкости 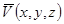определяет векторное поле. Он указывает направление в каждой точке, по которому стремится подвинуться частица жидкости, попавшая в эту точку.

Если поле скоростей с течением времени не меняется, то векторные линии будут служить траекториями жидких частиц и их называют линиями тока. Движение жидкости в этом случае называется стационарным.

Всякой дифференцируемой на области (то есть дифференциалу на скалярному полю) скалярной функции соответствует векторное поле ее градиентов

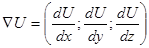
Уравнение касательной плоскости в точке 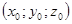к поверхности уровня скалярной функции 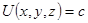, имеет вид:

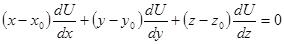
где значения частных производных функции 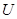берутся в точке 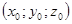. Следовательно, в силу геометрического смысла коэффициентов уравнения плоскости, видно, что градиент 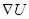перпендикулярен поверхности уровня плоскости, видно, что градиент 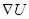перпендикулярен поверхности уровня функции .

Дата добавления: 2014-01-04