Функция, непре­рывная во всех точках замкнутой области G, называется непре­рывной в G

.

Это есть функция, определённая во всей плоскости комплексного переменного , кроме , многозначная, потому что каждый вектор имеет бесконечное множество различных направляющих углов, разнящихся друг от друга на кратное . Когда точка описывает окруж­ность, внутри которой лежит начало координат, то при одном положительном обходе этой окружности возрастает на , при n-кратном обходе—на . Если же точка описывает окружность, для которой нулевая точка будет внешней, то после обхода принимает первоначальное значе­ние.

Рис. 39.3.

Действительно, после обхода окружности (Рис. 39.3.) может при­нять лишь такое значение, которое разнится от начального значения на кратное . Однако вектор всё время остаётся в угле, образованном двумя касательными к окружности, проведёнными из точки ; следовательно, не может принимать значения, которые отличались бы от начального его значения больше, чем на угол между обеими касательными. Так как этот угол меньше , то при обходе указанной окружности должен вер­нуться к первоначальному значению. Отсюда следует, что можно рассматривать как однозначную непрерывную функцию в окрестности любой точки плоскости, не содержащей нулевой точки. Аналогично можно показать, что есть функция, однозначная и непрерывная во всякой односвязной области, не содержащей нулевой точки.

Иногда функция 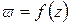рассматривается определённой также и в граничных точках области G, т. е. во всей замкнутой области G. Тогда под непрерывностью функции в граничной точке области G понимают следующее: условия непрерывности (39.3) и (39.4.) выполняются для всех точек , принадлежащих области G, т. е. точки , лежа­щие вне области G, оставляют вне рассмотрения.

Подобным же образом говорят также о непрерывности вдоль кривой, понимая под этим, что условия непрерывности (39.3.), (39.4.) выполняются только для точек, лежащих на рассматриваемой кривой, не обращая внимания на значения функции в других точках.

Так, в примере 39.1. функция непрерывна вдоль действитель­ной положительной оси во всякой точке этой линии, так как в этих точках она всё время равна нулю, несмотря на то, что эта функция не будет просто непрерывной ни в какой точке этой линии.

Дата добавления: 2014-01-04