Для всех , удовлетворяющих неравенству

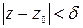(39.4.)

или, короче:

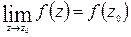(39.2а)

Геометрически это определение означает, что для всех точек , лежащих внутри круга 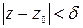с центром в точке достаточно малого радиуса , соответствующие значения функции изо­бражаются точками, лежащими внутри круга 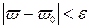с цент­ром в точке 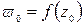сколь угодно малого радиуса . Мы можем формулировать короче определение непрерывности таким образом: функция называется непрерывной в точке , если для всех точек достаточно малой окрестности точки соответ­ствующие значения функции лежат в произвольно малой окрест­ности точки .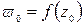

Функция, непрерывная в каждой точке области G, называется непрерывной в этой области.

Например, 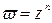непрерывна в каж­дой точке плоскости. Действительно, полагая имеем: 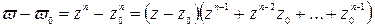; переходя к модулям, мы получим следующее не­равенство:

, где положено: .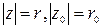

Рассматривая теперь окрестность точки , мы видим, что для всех точек этой окрестности имеет место очевидное неравенство 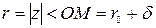(Рис. 39.2.)

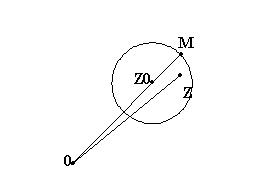
Рис. 39.2.

Поэтому будем иметь:

Отсюда ясно, что мы можем выбрать столь малым, чтобы 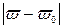был меньше любого наперёд заданного положительного числа .

Итак, 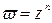есть функция, непрерывная во всей плоскости ком­плексного переменного .

Так как определение непрерывности функции комплексного пере­менного с формальной стороны аналогично соответствующему опреде­лению для функции действительного переменного, то доказательства теорем об операциях над непрерывными функциями остаются теми же в комплексной области, что и в действительном анализе.

Так, сум­ма, разность и произведение двух функций и , непрерыв­ных в точке (в области G), есть функция, непрерывная в той же точке (в той же области); также частное таких функ­ций есть функция, непрерывная в точке (в области G), е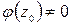сли [если в области G ].

Пользуясь этим предложе­нием, мы можем, например, заключить, что любая целая рациональ­ная функция 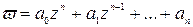непрерывна во всей пло­скости комплексного переменного .

Всякая рациональная функция непрерывна в каждой точке пло­скости комплексного переменного , за исключением тех значений , при которых знаменатель равен нулю.

Пример 39.1.

Это есть функция, однозначно определённая во всей плоскости комплексного переменного , непрерывная во всякой точке, отличной от то­чек действительной положительной оси. Будет ли функция непрерывной в этих последних точках?

Очевидно, нет, так как в противном случае для всех точек достаточно малой окрестности точки должно быть , что не выполняется, если точка нахо­дится на луче, для которого . Заметим, что если приближается к точ­ке 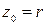вдоль положительной действительной оси 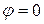, то условие не­прерывности выполняется, так как для таких точек все время 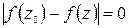и, значит, . Однако определение непрерывности функции 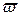в точке требует, чтобы при произвольном приближении точки к точке значение функции 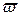стремилось к .

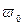Пример 39.2.

.

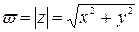Эта функция непрерывна во всей плоскости комплексного переменного , так как, очевидно, .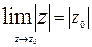

Пример 39.3.

Дата добавления: 2014-01-04