Понятие области. Линия Жордана

В предыдущем пункте мы считали функцию комплексного переменного определённой на некотором произвольном множестве точек Е. В дальнейшем мы почти исключительно будем принимать за множество точек Е, на кото­ром изменяется независимое переменное , так называемую область плоскости, определение которой мы и должны теперь дать. Предва­рительно выясним понятие внутренней точки множества.

Точку Р называют внутренней точкой множества Е, если все точки достаточно малого круга с центром в точке Р принадлежат этому множеству Е. Так, например, рассматривая все точки, заклю­чённые между двумя концентрическими окружностями, мы получаем множество, состоящее из одних внутренних точек. Присоединяя же к этому множеству точки, лежащие на окружности (на одной или обеих), мы будем иметь множество, которое содержит точки, не являющиеся для него внутренними: такими будут все точки, расположенные на окружностях.

Областью мы называем множество G точек плоскости, удовле­творяющее следующим двум условиям:

1) G состоит из одних внутренних точек,

2) любые две точки множества можно соединить ломаной с до­статочно большим числом звеньев так, чтобы все точки этой линии принадлежали самому множеству.

Так, вышеприведенный пример множества представляет область; во втором же случае мы не имеем области. Когда дана область G, то все точки плоскости можно разделить на два класса по отноше­нию к этой области. К первому классу мы отнесём все точки об­ласти G, ко второму – точки, не принадлежащие G. Очевидно, точка Q, не принадлежащая области G (точка второго класса), может быть двоякого типа: либо все точки достаточно малого круга с центром в этой точке Q не принадлежат области G, – такую точку Q мы назовём внешней точкой облает G, -либо, при сколь угодно малом круге с центром в точке Q, в этом круге будут всегда точки области G, – такую точку Q мы назовём граничной точкой области G. Совокупность всех граничных точек области G называют её границей. Единственным примером области без границы слу­жит вся расширенная плоскость комплексного переменного. Таким образом, отвлекаясь от этого случая, можно сказать, что всякая область G имеет границу. Существенно отметить, что не всегда существуют внешние точки области G; так, например, совокупность всех точек плоскости, не лежащих на отрезке действительной оси [–1, +1], представляет область, не имеющую внешних точек.

Множество, состоящее из области G и её границы, называется замкнутой областью и обозначается через .

Выяснив понятие области, перейдём к определению понятия не­прерывной линии в смысле Жордана. Пусть и суть действительные непрерывные функции переменного , изменяющегося на отрезке .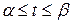

Два уравнения

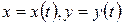
(39.1.)

дают параметрическое изображение непрерывной линии. Если мы по­требуем, чтобы двум различным значениям параметра (за исклю­чением, быть может, значений и 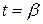, соответствующих на­чалу и концу линии) соответствовали всегда две различные точки линии, то наша линия не будет иметь кратных точек. Такую линию мы будем называть линией Жордана или просто непрерывной ли­нией. Если мы положим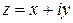, так что 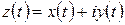, то её аналитическое изображение может быть записано с помощью одного уравнения:

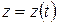
(39.1а.)

Когда параметр изменяется, возрастаяна отрезке ,точкаописывает линию Жордана, началом которой служит точка и концом точка 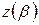; тем самым на линии (39.1а) устанавливается поло­жительное направление.

Геометрически линия Жордана, очевидно, представляет множе­ство точек плоскости, являющееся взаимно однозначным и непрерыв­ным отображением прямолинейного отрезка. Если начало и конец линии Жордана совпадают между собой, т. е.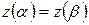, то она называется замкнутой. Как показал Жордан, непрерывная замкнутая линия без кратных точек делит плоскость на две разные области: одну, не содержащую бесконечно удалённой точки, называемую внутренней по отношению к данной линии, другую, содержащую бес­конечно удаленную точку и называемую внешней по отношению к данной кривой. Для обеих этих областей данная линия является границей. Мы будем предполагать, что вышеуказанное положитель­ное направление на линии выбрано так, что внутренняя часть кривой лежит слева от точки , движущейся в этом направлении. Замкну­тую линию Жордана геометрически мы можем рассматривать как взаимно однозначный и непрерывный образ окружности. Действи­тельно, не уменьшая общности, мы можем положить 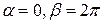и рассматривать параметр как аргумент точки окружности. Область, лежащая внутри замкнутой линии Жордана, обладает одним замеча­тельным свойством: какую бы замкнутую непрерывную линию мы ни провели в этой области, её внутренняя часть также принадлежит данной области.

Вообще, всякую область, обладающую этим свойством, мы назо­вём односвязной, а области, не обладающие упомянутым свойством, – многосвязными. Так, например, часть плоскости, лежащая внутри многоугольника, есть односвязная область, границей которой служит этот многоугольник: наоборот, часть плоскости, лежащая вне мно­гоугольника, будет многосвязной, так как внутренняя часть замкнутой жордановой кривой, окружающей многоугольник, не вся принадле­жит данной области. Точно так же многосвязной будет область, со­стоящая из точек кругового кольца .

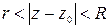Для областей, лежащих в расширенной плоскости, понятие одно­связности несколько обобщается. Именно, такая область называется односвязной, если для замкнутой жордановой кривой, принадлежащей области, либо внутренняя, либо внешняя часть (включая и бесконечно удалённую точку) принадлежит этой области. Например, внешняя часть многоугольника является здесь односвязной или многосвязной, смотря по тому, включаем ли мы в неё бесконечно удалённую точку или же исключаем.

Мы уже отметили, что часть плоскости, лежащая внутри произ­вольной замкнутой линии Жордана, есть односвязная область, грани­цей которой служит эта линия Жордана. Рассматривая области, границы которых состоят из нескольких замкнутых линий Жор­дана, мы будем иметь примеры многосвязных областей. Так, пусть суть замкнутые линии Жордана, такие, что каждая из линий 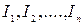лежит вне остальных и все они расположены внутри 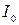(Рис.39.1.).

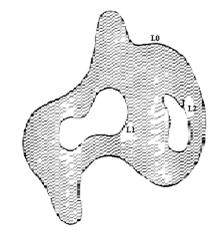
Рис. 39.1 Замкнутая область

Множество точек плоскости, лежащих одновременно внутри ли­нии 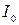и вне всех линий 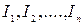будет представлять область, границей которой служит совокупность точек линий . Например, множество точек , удовлетворяющих неравенству 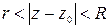, представляет область, граница которой состоит из двух окружностей радиусов г и R с общим центром в точке . При 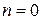мы имеем прежний про­стейший случай односвязной об­ласти.

Наоборот, в случае 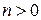в области существуют такие непре­рывные замкнутые линии, внутрен­ние части которых не целиком при­надлежат области. Таким образом, область, граница которой состоит из нескольких 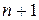замкнутых линий, будет многосвязной и именно 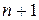- связной.

Например, множество точек, лежащих внутри кругового кольца, - двухсвязная область, область, изображённая на (Рис 39.1.),– трёхсвязная и т. д. Область называется ограниченной, если все её точки лежат внутри некоторого круга с центром s нулевой точке достаточно большого постоянного радиуса. В противном случае область называется не­ограниченной. В дальнейшем, если не оговорено противное, под сло­вом «область» мы будем понимать произвольную ограниченную или неограниченную область плоскости, односвязную или многосвязную, не содержащую бесконечно удалённой точки, и будем её обозначать через G. Множество точек, состоящее из точек области G и её гра­ничных точек, мы будем называть замкнутой областью и обозна­чать через .

Дата добавления: 2014-01-04