Понятие равномерно сходящегося ряда

Пусть имеем ряд

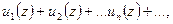(40.1.)

все члены которого суть однозначные функции комплексного пере­менного 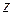, определённые в некоторой области G; предположим, что этот ряд сходится во всякой точке 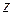области G. В этом случае сумма ряда (40.1.) будет однозначно определена в каждой точке 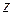области G и, следовательно, будет представлять однозначную функ­цию 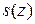в области G.

Предположим, что все члены сходящегося ряда (40.1.) суть непрерывные функции в области G; тогда возникает вопрос.

Пример 40.1.

Предполагая 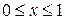, образуем ряд, сумма первых 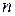членов которого равна 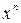. Это будет ряд

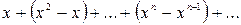(40.2.)

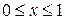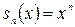Если , то стремится к нулю при неограниченном возрастании 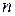; если же 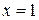, то и 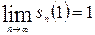. Следовательно, сумма рассматриваемого ряда 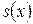равна нулю при 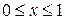и равна единице при 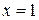. Итак, сумма 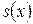имеет точку разрыва при 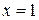, несмотря на то, что данный ряд сходится в каждой точке отрезка 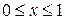и все его члены –непрерывные функции. Этот пример можно, конечно, рассматривать и с точки зрения комплекс­ного переменного, если заметить, что .

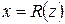Пример 40.2.

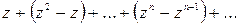
Предполагая 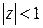или 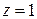. Если 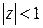, то сумма его первых 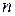членов 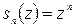стремится к нулю при неограниченном возраста­нии 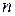, потому что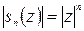. Если же 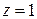, то , и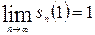l. Итак, сумма рассматриваемого ряда 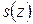равна нулю во всякой точке 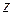, лежащей внутри круга 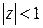, и равна единице в точке 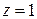окружности этого круга. Здесь, как и в первом примере, функция 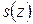оказывается разрывной при 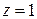и изобра­жается в виде суммы сходящегося ряда непрерывных функций.

Итак, для того чтобы сумма сходящегося ряда непрерывных функ­ций была непрерывной функцией, нужно на этот ряд наложить допол­нительное ограничение. Таким ограничением может служить условие равномерной сходимости ряда. Обозначая через 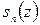сумму первых 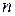членов данного ряда, сходящегося в области G, рас­смотрим разность 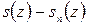, которая вследствие сходимости ряда стремится к нулю при неограниченном возрастании 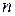для любой точки 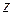области G. Это значит, что выполняемся неравенство

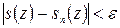(40.3.)

где 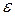— сколь угодно малое положительное число, если 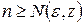. При изменении точки 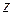в области G может случиться, что принимает сколь угодно большие значения. В этом случае нельзя найти такое число 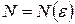, начиная с которого выполнялось бы неравенство (40.3.) во всей области G. Другая возможность состоит в том, что для всех точек области G остается меньше некоторого числа 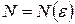. В этом случае неравенство (40.3.) выпол­няется для всех рассматриваемых точек 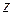при 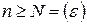; в этом случае говорят, что данный ряд (40.3.) сходится равномерно в области G к функции .

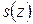Итак, ряд (40.1.), по определению, сходится равномерно в области G к функции 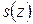, если для всякого сколь угодно малого положитель­ного числа 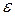можно найти такое натуральное число 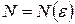, что при всех 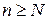выполняется неравенство 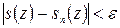, какова бы ни была точка 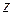в области G.

Иными словами, в случае равномерной сходимости ряда его сумму можно аппроксимировать с любой степенью точности 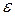посредством суммы одного и того же числа 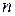первых членов, принимая .

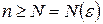В примере 40.2. 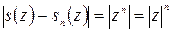, если .

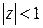Для того чтобы выполнялось неравенство 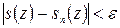, нужно потребовать, чтобы было 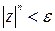, откуда 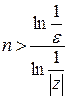. Обозначая через наибольшее целое число, содержащееся в количестве 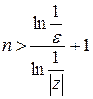, мы видим, что для выполнения неравенства (40.3.) необходимо, чтобы было 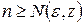. Когда 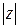стремится к единице, то стре­мится к бесконечности, и, следовательно, нельзя указать натуральное число N, которое было бы больше, чем , для любого , .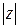

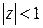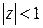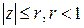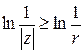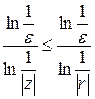Следовательно, этот ряд не будет равномерно сходиться в круге . Однако этот ряд будет равномерно сходящимся во всяком круге |. В самом деле, так как ,то , и, следовательно, обозначая через 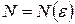наибольшее натуральное число, содержащееся в выражении 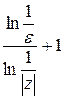имеем: 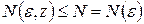, каково бы ни было , .

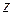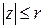Дата добавления: 2014-01-04