Признак равномерно сходящегося ряда

Ряд функций, непрерывных в области G, рав­номерно сходящийся в этой области, изображает функцию, непре­рывную в той же области.

Действительно, так как все члены ряда суть непрерывные функ­ции в каждой точке области G, то согласно теореме сумма ряда должна быть непрерывной функцией в каждой точке области G, т.е. всюду в области.

Весьма часто можно заключить о равномерной сходимости ряда (40.1.) на основании следую­щего простого признака:

Если все члены ряда (40.1.) в областиG удовлетворяют условию

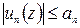, (40.8.)

где 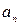– постоянные положительные числа, причём числовой ряд

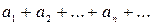(40.9.)

сходится, то данный ряд (40.1.) сходится равномерно (и притом абсолютно) в области G. Действительно, ряд

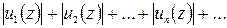
сходится во всякой точке 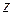области G, так как его члены не больше соответствующих членов 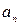сходящегося ряда (40.9.). Следовательно, данный ряд (40.1.) абсолютно сходится в каждой точке 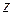области G,. Обозначая через 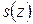и 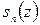соответственно сумму ряда (40.1.) и сумму первых 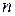его членов, получим:

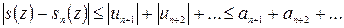(40.10.)

Так как ряд (40.9.), по условию, сходится, то его остаточный член 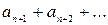будет меньше 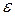, каково бы ни было 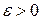, начи­ная с достаточно большого .

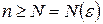Таким образом, из неравенства (40.10.) получаем:

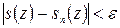при ,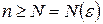

независимо от точки 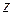области G, что и доказывает равномерную сходимость ряда (40.1.) в области G. В качестве примера рассмотрим ряд

,

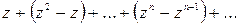равномерную сходимость, которую мы уже обнаружили при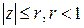

Здесь ,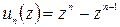

следовательно: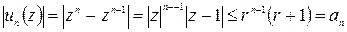

Так как ряд с общим членом 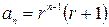при 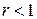сходится как бесконечно убывающая геометрическая прогрессия, то на осно­вании доказанного признака рассматриваемый ряд должен сходиться равномерно (и абсолютно) при .

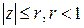Дата добавления: 2014-01-04