
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Простейшие дифференциальные уравнения первого порядка
|
|
|
|
Упражнения
1. Решить дифференциальное уравнение  .
.
Ответ:  - общее решение.
- общее решение.
2. Решить дифференциальное уравнение  .
.
Ответ:  - общее решение.
- общее решение.
3. Решить дифференциальное уравнение  .
.
Ответ:  - общее решение; у =1 – особое решение.
- общее решение; у =1 – особое решение.
Это - дифференциальные уравнения вида
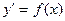 (4)
(4)
Решение такого уравнения очевидно: всякая функция 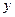 , удовлетворяющая этому уравнению, является первообразной для функции
, удовлетворяющая этому уравнению, является первообразной для функции 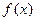 . А значит, любое частное решение
. А значит, любое частное решение 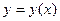 этого уравнения может быть найдено в результате интегрирования функции
этого уравнения может быть найдено в результате интегрирования функции 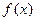 :
:
 (5)
(5)
Формула (5) представляет собой общее решение уравнения (4). Она содержит в себе все частные решения этого уравнения. Особых решений у уравнения (4) нет.
Дифференциальные уравнения с разделяющимися переменными
Это – дифференциальные уравнения вида
 (6)
(6)
Решение таких уравнений производится по следующей схеме.
1) Сначала находим такие числовые значения 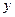 , при которых
, при которых 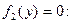
 (7)
(7)
Функции  являются, очевидно, частными решениями уравнения (6), ибо при подстановке каждой из них в это уравнение получим тождество 0=0.
являются, очевидно, частными решениями уравнения (6), ибо при подстановке каждой из них в это уравнение получим тождество 0=0.
2) Теперь находим все остальные решения 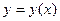 уравнения (6), для которых
уравнения (6), для которых 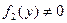 . Делаем это по схеме:
. Делаем это по схеме:

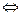 | разделим выражения с х и у (разделим переменные х и у)) |
| разделим выражения с х и у (разделим переменные х и у)) |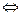
 | интегрируем обе части |
| интегрируем обе части |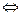
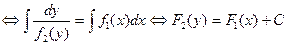 (8)
(8)
Полученное равенство  представляет собой общее решение уравнения (6) в неявном виде (его общий интеграл). Если в нем можно выразить
представляет собой общее решение уравнения (6) в неявном виде (его общий интеграл). Если в нем можно выразить 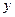 , приводим его к явному виду
, приводим его к явному виду .
.
Пример 4. Решить дифференциальное уравнение  .
.
Решение. Данное уравнение – уравнение вида  при
при  и
и 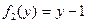 , то есть это уравнение с разделяющимися переменными. Решим его по изложенной выше схеме.
, то есть это уравнение с разделяющимися переменными. Решим его по изложенной выше схеме.
1)  .
.
Итак, одно частное решение уравнения  уже найдено: это функция
уже найдено: это функция 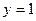 .
.
2) Найдём по схеме (8) общее решение этого уравнения, содержащее все его остальные частные решения:
 | разделяем переменные х и у |
| разделяем переменные х и у |

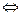 | интегрируем обе части |
| интегрируем обе части |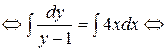
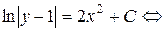
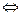

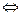 | неопределенную константу
| неопределенную константу 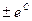 опять обозначим буквой С |
опять обозначим буквой С |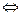
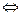
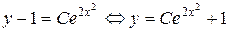
Последнее равенство и есть искомое общее решение в явном виде. Отметим, что при С =0 из него получается и найденное в пункте 1 частное решение 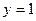 . Таким образом, общее решение
. Таким образом, общее решение  уравнения
уравнения  содержит все его частные решения.
содержит все его частные решения.
Однородные дифференциальные уравнения 1-го порядка.
Это – дифференциальные уравнения вида
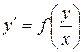 (9)
(9)
Такие уравнения сводятся к уравнениям (6) с разделяющимися переменными после введения новой известной функции  . Действительно, пусть
. Действительно, пусть
 тогда
тогда 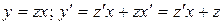 (10)
(10)
С учетом равенств (10) уравнение (9) примет вид:
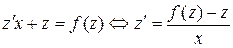 (11)
(11)
А это - уравнение вида 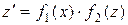 при
при 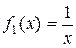 и
и  , то есть уравнение с разделяющимися переменными для новой неизвестной функции
, то есть уравнение с разделяющимися переменными для новой неизвестной функции 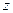 . Найдя все его решения
. Найдя все его решения  , затем по формуле
, затем по формуле  найдем и все решения
найдем и все решения 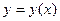 исходного уравнения (9).
исходного уравнения (9).
Пример 5. Решить дифференциальное уравнение первого порядка
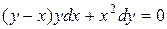
Решение. Сначала убедимся в том, что это действительно дифференциальное уравнение первого порядка, а заодно и определим его тип:
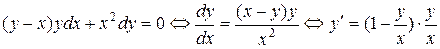
Это – уравнение вида 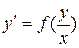 , то есть однородное дифференциальное уравнение первого порядка. Для его решения введем вместо
, то есть однородное дифференциальное уравнение первого порядка. Для его решения введем вместо 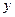 новую известную функцию
новую известную функцию 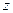 :
:
 ; тогда
; тогда 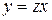 , а
, а 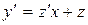
С учетом этого наше дифференциальное уравнение примет вид:
 .
.
Это – уравнение вида  при
при  и
и  , то есть уравнение с разделяющимися переменными. Решим его по соответствующей таким уравнениям схеме.
, то есть уравнение с разделяющимися переменными. Решим его по соответствующей таким уравнениям схеме.
1)  .
.
Итак, одно частное решение 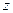 уже найдено: это функция
уже найдено: это функция  .
.
2) Найдем общее решение уравнения 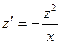 , содержащее все его остальные частные решения:
, содержащее все его остальные частные решения:
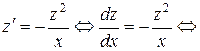 | разделяем переменные
| разделяем переменные  и
и 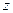 |
| 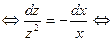
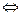 | интегрируем обе части |
| интегрируем обе части | 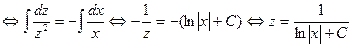
Это – общее решение уравнения  . Заметим, что найдено в пункте 1 частное решение
. Заметим, что найдено в пункте 1 частное решение  этого уравнения не получается из общего решения
этого уравнения не получается из общего решения 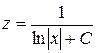 ни при каком значении С. Следовательно,
ни при каком значении С. Следовательно,  – это особое решение указанного уравнения.
– это особое решение указанного уравнения.
Ну а теперь, найдя все функции  и учитывая, что
и учитывая, что 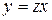 , можем записать и все функции
, можем записать и все функции 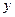 , то есть все решения исходного дифференциального уравнения:
, то есть все решения исходного дифференциального уравнения:
 - общее решение;
- общее решение;  – особое решение.
– особое решение.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 635; Нарушение авторских прав?; Мы поможем в написании вашей работы!