Признак Вейерштрасса

Теорема 40.1. Если числовой ряд 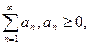сходится и для всех 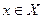и для всех п = 1, 2,… выполняется неравенство 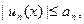то ряд сходится абсолютно и равномерно на множестве Х.

Доказательство.

Для любого ε > 0 cуществует такой номер N, что 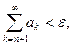поэтому 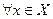и

для остатков r_n ряда справедлива оценка

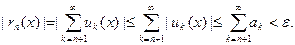Следовательно, 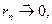поэтому ряд равномерно сходится.

Замечание. Процедура подбора числового ряда, отвечающего условиям теоремы 40.1, обычно называется мажорированием, а сам этот ряд – мажорантой для данного функционального ряда.

Пример. Для функционального ряда 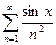мажорантой при любом значении х является сходящийся знакоположительный ряд 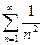. Поэтому исходный ряд равно-мерно сходится на (-∞, +∞).

Дата добавления: 2014-01-04