Понятие функции, аналитической в области

Производная функций комплексного переменного.

Определение. Производной от однозначной функции w = f(z) в точке z называется предел:

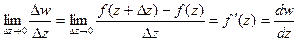
Определение. Функция f(z), имеющая непрерывную производную в любой точке области D называется аналитической функцией на этой области.

Правила дифференцирования функций комплексного аргумента не отличаются от правил дифференцирования функций действительной переменной.

Аналогично определяются производные основных функций, таких как синус, косинус, тангенс и котангенс, степенная функция и т.д.

Производные гиперболических функций определяются по формулам:

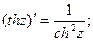
Вывод правил интегрирования, значений производных основных функций ничем не отличается от аналогичных операций с функциями действительного аргумента, поэтому подробно рассматривать их не будем.

Таким образом, функция может быть аналитической только в не­которой области; однако и о каждой отдельной точке такой области говорят, что в ней наша функция аналитическая. При этом важно заметить, что функция, аналитическая в точке, по определению дол­жна быть аналитической в некоторой окрестности этой точки.

Пример 43.1.

Функция , непрерывная во всей плоскости, имеет в точке 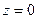производную, равную нулю, потому что отношение 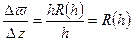стремится к нулю вместе с . Эта функция, моногенная в нулевой точке, не будет аналитической в этой точке, так как в любой другой точке плоскости эта функция не будет диф­ференцируемой.

В самом деле, отношение

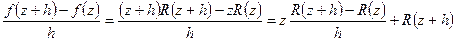
при 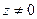не стремится к определённому пределу, когда стремится к нулю. Это будет очевидным, если положим 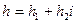и заметим,

что отношение

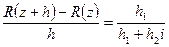
имеет предел, равный единице при 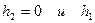стремящемся к нулю, и это же отношение стремится к нулю при 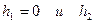стремящемся к нулю.

Приведённый пример даёт функцию, непрерывную во всей пло­скости и нигде не дифференцируемую, кроме 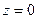. Взяв аналогично предыдущему, мы показали бы, что эта функция, непре­рывная во всей плоскости, нигде не дифференцируема.

Другим при­мером непрерывной и нигде не дифференцируемой функции может служить: 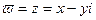. Таким образом, мы видим, что весьма легко образовать примеры непрерывных функций комплексного переменного, лишённых производных в каждой точке плоскости. Простота образо­вания таких функций объясняется тем, что требование дифференцируемости функции в точке по комплексному переменному гораздо более сильное, нежели по действительному переменному. Действи­тельно, предполагая дифференцируемость функции 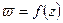в точке 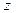, мы считаем, что предел отношения 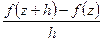будет одним и тем же числом независимо от направления, по которому переменная точка 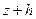приближается к постоянной точке .

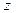Ещё более сильным будет требование дифференцируемости функции в каждой точке области; отсюда становится понятным, что функции, аналитические в области, должны обладать рядом специфических свойств, присущих только им одним среди множества всех функций комплексного переменного. Основная задача настоящего руководства и состоит в том, чтобы выявить основные замечательные свойства таких функций. Так как определение производной функции комплексного переменного совер­шенно аналогично с формальной стороны соответствующему определению для функции действительного переменного, то все известные из дифференциального исчисления правила дифференцирования легко могут быть перенесены в комплексную область. Отсюда, в частности, следует, что целая рациональная функция есть аналитическая во всей плоскости; функция рациональная есть аналитическая во всей пло­скости комплексного переменного, кроме точек, в которых её зна­менатель обращается в нуль.

Дата добавления: 2014-01-04