
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 44
|
|
|
|
Показательная функция. Функции тригонометрические и гиперболические.
Мы видели, что степенные ряды
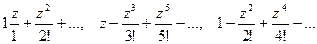
сходятся абсолютно во всей плоскости комплексного переменного 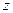 . Суммы таких рядов будут, как мы только что видели, функциями комплексного переменного
. Суммы таких рядов будут, как мы только что видели, функциями комплексного переменного 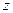 , аналитическими во всей плоскости. Из анализа известно, что если
, аналитическими во всей плоскости. Из анализа известно, что если 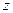 принимает действительные значения
принимает действительные значения  , то суммы этих рядов суть соответственно
, то суммы этих рядов суть соответственно  Условимся при любом комплексном значении
Условимся при любом комплексном значении 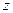 суммы наших рядовобозначать соответственно через
суммы наших рядовобозначать соответственно через , т.е. положим:
, т.е. положим:


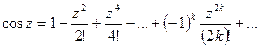
Таким образом, мы определим три функции комплексного переменного 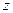 , аналитические во всей плоскости. Покажем, что известные в случае действительного
, аналитические во всей плоскости. Покажем, что известные в случае действительного 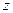 свойства этих функций распространяются на случай любого комплексного
свойства этих функций распространяются на случай любого комплексного 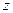 .
.
Так, формула умножения показательной функции

 (44.1.)
(44.1.)
доказывается для любых комплексных 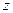 и
и  посредством умножения соответствующих рядов. Заметив, что
посредством умножения соответствующих рядов. Заметив, что

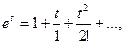
получаем: 
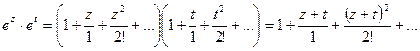
Ряд, стоящий в правой части последнего равенства, получается из ряда для 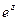 заменой
заменой 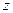 на
на 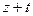 ; следовательно, его сумма равна
; следовательно, его сумма равна  , и формула (44.1.) доказана. Полагая в формуле, (44.1.)
, и формула (44.1.) доказана. Полагая в формуле, (44.1.)  , найдём:
, найдём:  ,
,
откуда
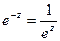 (44.2.)
(44.2.)
Пользуясь формулой (44.2.), легко вывести формулу деления показательной функции:
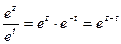
т.е.
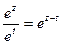 (44.3.)
(44.3.)
В действительной области тригонометрические функции 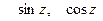 не связаны с показательной функцией
не связаны с показательной функцией 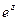 . Рассматривая эти функции в комплексной области, Эйлер установил замечательное соотношение между ними:
. Рассматривая эти функции в комплексной области, Эйлер установил замечательное соотношение между ними:
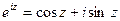 (44.4.)
(44.4.)
Для доказательства тождества (44.4.) заменим в ряде для 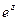 букву
букву 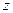 через
через 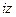 и соберём отдельно члены, не содержащие
и соберём отдельно члены, не содержащие 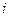 , и члены, содержащие
, и члены, содержащие 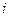 ; получим:
; получим:
 .
.
Заметив, что ряд, стоящий в скобках, выражает 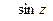 , а ряд, стоящий вне скобок, определяет
, а ряд, стоящий вне скобок, определяет 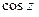 , получаем тождество (44.4.); Так как ряд для
, получаем тождество (44.4.); Так как ряд для 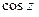 содержит лишь чётные степени
содержит лишь чётные степени 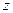 , а ряд, выражающий
, а ряд, выражающий 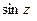 , – лишь нечётные степени
, – лишь нечётные степени 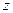 , то имеем:
, то имеем:
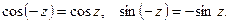
Заменяя в тождестве Эйлера (44.4.) 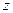 на
на  , получаем:
, получаем:
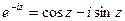 (44.4.а.)
(44.4.а.)
Складывая тождества (44.4.) и (44.4.а.), находим:
 (44.5.)
(44.5.)
Вычитанием же их получаем:
 (44.5.а.)
(44.5.а.)
Эти формулы также носят имя Эйлера.
Пользуясь тождеством Эйлера, легко доказать, что показательная функция 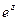 имеет период
имеет период 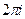 . Действительно, с одной стороны, по формуле (44.1.) имеем:
. Действительно, с одной стороны, по формуле (44.1.) имеем: 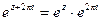 , с другой стороны, в силу тождества (44.4.) имеем:
, с другой стороны, в силу тождества (44.4.) имеем:  . Следовательно, получаем:
. Следовательно, получаем: 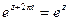 , т. е. функция
, т. е. функция 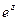 не изменяет своего значения при прибавлении к независимому переменному постоянного числа
не изменяет своего значения при прибавлении к независимому переменному постоянного числа 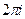 .
.
Наконец, пользуясь тождеством Эйлера, получаем так называемую показательную форму для представления любого комплексного числа: 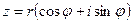 ,
,
Откуда
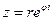 (44.6.)
(44.6.)
Известные из тригонометрии формулы сложения и вычитания синуса и косинуса
 (44.7.)
(44.7.)
 (44.8.)
(44.8.)
распространяются и на комплексную область.
В самом деле, по формуле (44.1.) имеем:  , откуда в силу тождества Эйлера получим:
, откуда в силу тождества Эйлера получим:
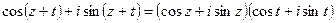 (44.9.)
(44.9.)
Изменяя в тождестве (44.9.) знаки у 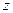 и
и  , найдём:
, найдём:
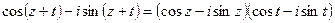 . (44.10.)
. (44.10.)
Раскрывая скобки в равенствах (44.9.) и (44.10.) и складывая их между собой, получим:
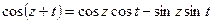 ;
;
вычитанием же равенств (44.9.) и (44.10.) найдём:
 .
.
Итак, мы вывели формулы сложения для косинуса и синуса. Формулы вычитания получатсяиз формул сложения заменой  на
на  . Наконец, полагая в формулах сложения
. Наконец, полагая в формулах сложения  , получим:
, получим:
 ,
,
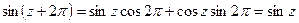 ,
,
т.е. число 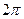 есть период синуса и косинуса и в комплексной области;
есть период синуса и косинуса и в комплексной области;
полагай же в формуле косинуса разности (44.7.)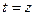 , найдём:
, найдём:
 . (44.11.)
. (44.11.)
Таким образом, мы видим, что все формулы тригонометрии остаются в силе и для комплексной области.
Отметим ещё, что показательная функция 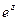 не обращается в нуль нигде на плоскости. В самом деле, полагая
не обращается в нуль нигде на плоскости. В самом деле, полагая 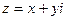 , имеем:
, имеем:
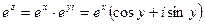 , откуда следует, что модуль функции
, откуда следует, что модуль функции 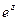 равен
равен  . При любом действительном значении
. При любом действительном значении  выражение
выражение 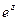 не равно нулю, а следовательно,
не равно нулю, а следовательно, не может сделаться нулём.
не может сделаться нулём.
Определим, наконец, все те точки плоскости, в которых  и
и  обращаются в нуль. В силу формулы (44.5.а.) равенство
обращаются в нуль. В силу формулы (44.5.а.) равенство  равносильно уравнению
равносильно уравнению 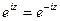 , или
, или 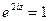 . Полагая
. Полагая  , находим:
, находим:
 (44.12.)
(44.12.)
В уравнении (44.12.) справа стоит единица, а слева – комплексное число, модуль которого равен  , аргумент же
, аргумент же 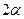 . Следовательно, имеем:
. Следовательно, имеем:  , где
, где 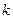 – целое число, откуда находим:
– целое число, откуда находим: 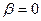 ,
,  . Итак, нули
. Итак, нули  будут:
будут: 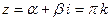 , где
, где 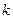 – любое целое число. Аналогично покажем, что все нули
– любое целое число. Аналогично покажем, что все нули  будут:
будут: , где
, где 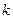 – любое целое число.
– любое целое число.
Заметим, что для комплексных значений аргумента уже нельзя более утверждать, что 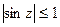 и
и  . В самом деле, например,
. В самом деле, например,  .
.
Согласно определению гиперболические синус и косинус будут:
 (44.13.)
(44.13.)
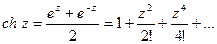 (44.14.)
(44.14.)
Сравнивая формулы (44.13.) и (44.14.) соответственно с формулами (44.5.а.) и (44.5.), получим:
 (44.15.)
(44.15.)
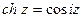 (44.16)
(44.16)
Эти формулы показывают, что гиперболические синус и косинус могут быть выражены посредством круговых синуса и косинуса, если воспользоваться комплексными числами. Записав формулы (44.15.) и (44.16.) в виде

и полагая 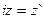 , имеем:
, имеем:
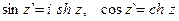 (44.16.)
(44.16.)
Отсюда вытекает следующее: любое соотношение между тригонометрическими функциями  и
и  переходит в соответствующее соотношение между гиперболическими функциями
переходит в соответствующее соотношение между гиперболическими функциями  и
и  , если в этом соотношении мы заменим
, если в этом соотношении мы заменим  через
через 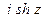 , a
, a  через
через  .
.
Таким образом, параллельно формулам обычной тригонометрии мы получаем все формулы гиперболической тригонометрии.
Отметим ещё формулы дифференцирования введённых нами функций. По доказанному в п. 6 этого параграфа производную от суммы степенного ряда можно получить, почленно дифференцируя степенной ряд, т. е.
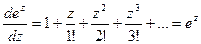 ,
, 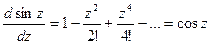 ,
,  ,
, 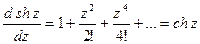 ,
,
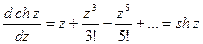 .
.
Таким образом, формулы дифференцирования, установленные для действительных значений аргумента, остаются в силе и для комплексных значений аргумента.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 237; Нарушение авторских прав?; Мы поможем в написании вашей работы!