Метод вариации произвольных постоянных

Лекция 44. Линейные неоднородные уравнения второго порядка. Метод вариации произвольных постоянных. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами. (специальная правая часть).

Социальные преобразования. Государство и церковь.

Социальная политика большевиков во многом диктовалась их классовым подходом. Декретом от 10 ноября 1917 г. уничтожена сословная система, от­менены дореволюционные чины, титулы и награды. Установлена выборность судей; проведена секуляризация гражданских состояний. Установлено бес­платное образование и медицинское обслуживание (декрет от 31 октября 1918 г.). Женщины уравнивались в правах с мужчинами (декреты от 16 и 18 декабря 1917 г.). Декрет о браке вводил институт гражданского брака.

Декретом СНК от 20 января 1918 года церковь отделена от государства и от системы образования. Большая часть церковного имущества конфискована. Патриарх Московский и всея Руси Тихон (избран 5 ноября 1917 года) 19 января 1918 года предал анафеме Советскую власть и призвал к борьбе против большевиков.

Рассмотрим линейное неоднородное уравнение второго порядка

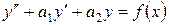(1)

Структура общего решения такого уравнения определяется следующей теоремой:

Теорема 1. Общее решение неоднородного уравнения (1) представляется как сумма какого-нибудь частного решения этого уравнения 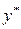и общего решения 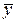соответствующего однородного уравнения

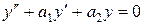(2)

Доказательство. Нужно доказать, что сумма

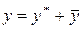(3)

есть общее решение уравнения (1). Докажем сначала, что функция (3) есть решение уравнения (1).

Подставляя сумму 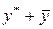в уравнение (1) вместо у, будем иметь

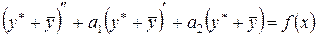
или

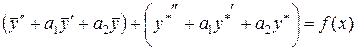(4)

Так как 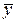есть решение уравнение (2), то выражение, стоящее в первых скобках, тождественно равно нулю. Так как 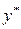есть решение уравнения (1), то выражение, стоящее во вторых скобках, равно f(x). Следовательно, равенство (4) является тождеством. Таким образом, первая часть теоремы доказана.

Докажем второе утверждение: выражение (3) есть общее решение уравнения (1). Мы должны доказать, что входящие в это выражение произвольные постоянные можно подобрать так, чтобы удовлетворялись начальные условия:

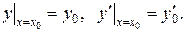(5)

каковы бы ни были числа х₀, y₀ и 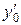(лишь бы х₀ было взято из той области, где функции а₁, а₂ и f(x) непрерывны).

Заметив, что 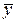можно представить в форме 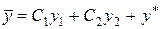. Тогда на основании условий (5) будем иметь

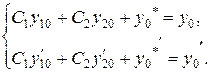
Решим эту систему и определим С₁ и С₂. Перепишем систему в виде:

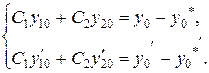(6)

Заметим, что определитель этой системы есть определитель Вронского для функций у₁ и у₂ в точке х=х₀. Так как эти функции по условию линейно независимы, то определитель Вронского не равен нулю; следовательно система (6) имеет определенное решение С₁ и С₂, т.е. существуют такие значения С₁ и С₂, при которых формула (3) определяет решение уравнения (1), удовлетворяющее данным начальным условиям. Что и требовалось доказать.

Перейдем к общему методу нахождения частных решений неоднородного уравнения.

Напишем общее решение однородного уравнения (2)

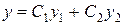. (7)

Будем искать частное решение неоднородного уравнения (1) в форме (7), рассматривая С₁ и С₂ как некоторые пока неизвестные функции от х.

Продифференцируем равенство (7):

.

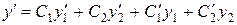Подберем искомые функции С₁ и С₂ так, чтобы выполнялось равенство

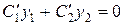. (8)

Если учесть это дополнительное условие, то первая производная примет вид

.

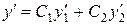Дифференцируя теперь это выражение, найдем :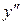

.

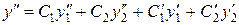Подставляя 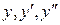в уравнение (1), получим

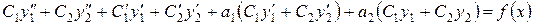
или

.

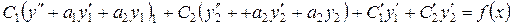Выражения, стоящие в первых двух скобках, обращаются в нуль, так как y₁ и y₂ – решения однородного уравнения. Следовательно, последнее равенство принимает вид

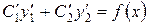. (9)

Таким образом, функция (7) будет решением неоднородного уравнения (1) в том случае, если функции С₁ и С₂ удовлетворяют уравнениям (8) и (9). Составим систему уравнений из уравнений (8) и (9).

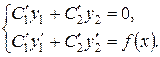
Так как определителем этой системы является определитель Вронского для линейно независимых решений y₁ и y₂ уравнения (2), то он не равен нулю. Следовательно, решая систему, мы найдем 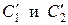как определенные функции от х:

.

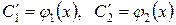Интегрируя, получим

,

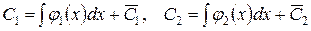где 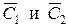- постоянные интегрирования.

Подставляя полученные выражения С₁ и С₂ в равенство (7), найдем интеграл, зависящий от двух произвольных постоянных 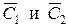, т.е. общее решение неоднородного уравнения.

Пример 1. Найти общее решение уравнения .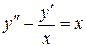

Решение. Найдем общее решение однородного уравнения 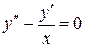. Так как , то ; .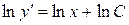

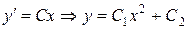Чтобы последнее выражение было решением данного уравнения, надо определять С₁ и С₂ как функции от х из системы

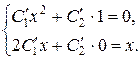
Решая эту систему, найдем , откуда в результате интегрирования получаем 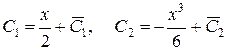. Далее подставим найденные функции в формулу 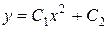, получаем общее решение неоднородного уравнения 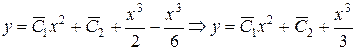, где 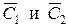- произвольные постоянные.

Дата добавления: 2014-01-04