Линейные неоднородные уравнения второго порядка с постоянными коэффициентами. ( специальная правая часть )

Пусть имеем уравнение

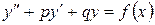(10)

где p и q – действительные числа.

У таких уравнений частное решение иногда бывает возможно найти проще, не прибегая к интегрированию. Это возможность зависит от вида правой части. Рассмотрим два случая:

1) Пусть правая часть уравнения (10) представляет собой произведение показательных функций на многочлен, т.е. имеет вид

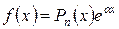(11)

где 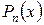- многочлен n –oй степени. Тогда возмлжны следующие частные случаи:

а) Число 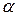не является корнем характеристического уравнения

.

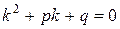В этом случае частное решение нужно искать в виде

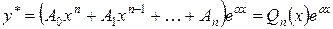. (12)

Действительно, подставляя 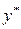в уравнение (10) и сокращая все члены на множитель 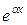, будем иметь:

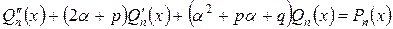. (13)

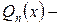многочлен степени n, 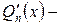многочлен степени n-1, 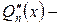многочлен степени n-2. Таким образом, слева и справа от знака равенства стоят многочлены n – oй степени. Приравнивая коэффициенты при одинаковых степенях х (число неизвестных коэффициентов равно n+1), получим систему n+1 уравнений для определения неизвестных коэффициентов А₀, А₁,А₂, …,А_n.

б) Число 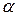есть простой (однократный) корень характеристического уравнения.

Если бы в этом случае частное решение мы стали искать в форме (12), то и в равенстве (13) слева получился бы многочлен степени n-1, так как коэффициент при 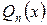, т.е. 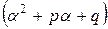, равен нулю, а многочлены 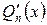и имеют степень, меньшую чем n. Следовательно, ни при каких А₀, А₁,А₂, …,А_n равенство (13) не было бы тождеством. Поэтому в рассматриваемом случае частное решение нужно брать в виде многочлена (n+1) –й степени, но без свободного члена. (так как свободный член этого многочлена исчезнет при дифференцировании).

.

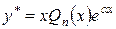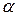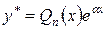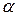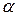в) Число есть двукратный корень характеристического уравнения. Тогда в результате подстановки в дифференциальное уравнение функции степень понижается на две единицы. Действительно, если - корень характеристического уравнения, то кроме того, так как является двукратным корнем, то 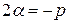(так как по теореме Виета сумма корней приведенного квадратного уравнения равна коэффициенту при неизвестном в первой степени, взятому с обратным знаком). Таким образом, .

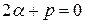Следовательно, в левой части равенства (13) остается , т.е. многочлен (n-2) –й степени. Для того, чтобы в результате подстановки получить многочлен степени n, следует частное решение искать в виде произведения 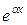на многочлен (n+2) –й степени. При этом свободный член этого многочлена и член в первой степени исчезнут при дифференцировании; поэтому их можно не включать в частное решение.

Итак, в случае, когда 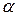является двукратным корнем характеристическим уравнения, частное решение можно брать в форме

.

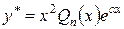Пример 2. Найти общее решение уравнения .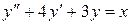

Решение. Найдем общее решение соответствующего однородного уравнения

.

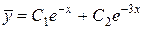Так как правая часть данного неоднородного уравнения имеет вид 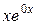(т.е. 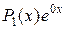), а 0 в показателе степени не является корнем характеристического уравнения , то частное решение будем искать в форме

.

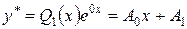Подставляя это выражение в заданное уравнение, будем иметь

.

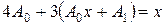Приравнивая коэффициенты при одинаковых степенях х, получим

,

откуда

.

Следовательно,

.

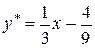Общее решение .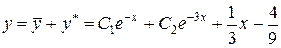

Пример 3. Найти общее решение уравнения .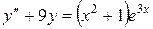

Решение. Найдем общее решение соответствующего однородного уравнения

.

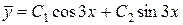Так как правая часть данного неоднородного уравнения имеет вид 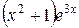(т.е. 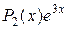), а 3 в показателе степени не является корнем характеристического уравнения 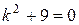, то частное решение будем искать в форме

.

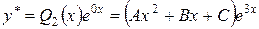Подставляя это выражение в заданное уравнение, будем иметь

.

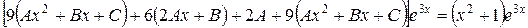Сокращая на 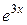и приравнивая коэффициенты при одинаковых степенях х, получим

,

откуда 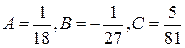. Следовательно, частное решение

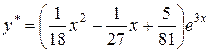
и общее решение .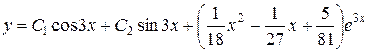

Пример 4. Найти общее решение уравнения .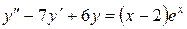

Решение. Найдем общее решение соответствующего однородного уравнения

.

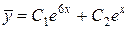Так как правая часть данного неоднородного уравнения имеет вид 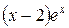(т.е. 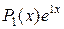), а коэффициент 1 в показателе степени является простым корнем характеристического уравнения , то частное решение будем искать в форме

.

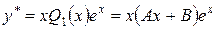Подставляя это выражение в заданное уравнение, будем иметь

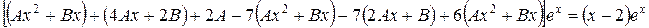или

.

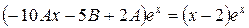Приравнивая коэффициенты при одинаковых степенях х, получим

,

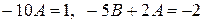откуда 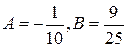. Следовательно, частное решение

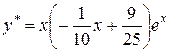
и общее решение .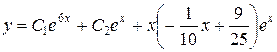

Переходим ко второму случаю, второму виду правой части.

2) Пусть правая часть уравнения (10) имеет вид

,

где 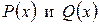- многочлены. Тогда форма частного решения определяется иак:

а) если число 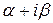не является корнем характеристического уравнения, то частное решение уравнения (10) следует искать в виде

,

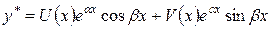где 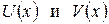- многочлены, степень которых равна наивысшей степени многочленов .

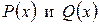б) если число 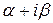есть корень характеристического уравнения, то частное решение уравнения (10) следует искать в виде

,

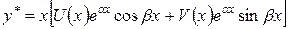где 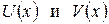- многочлены, степень которых равна наивысшей степени многочленов .

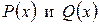При этом указанные формы частных решений сохраняются и в тех случаях, когда в правой части уравнения (10) один из многочленов 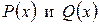тождественно равен нулю, т.е. когда правая часть имеет вид или .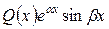

Пример 5. Найти общий интеграл линейного неоднородного уравнения .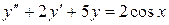

Решение. Характеристическое уравнения 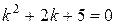имеет корни 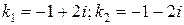. Поэтому общий интеграл соответствующего однородного уравнения

.

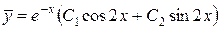Частное решение неоднородного уравнения ищем в виде

,

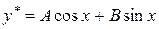где А и В – постоянные коэффициенты, подлежащие определению. Подставляя 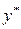- в заданное уравнение, будем иметь

.

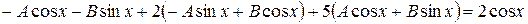Приравнивая коэффициенты при cosx и sinx, получим два уравнения для определения А и В:

-А+2В+5А=2, -В-2А+5В=0,

откуда А=2/5,В=1/5. Общее решение данного уравнения:

.

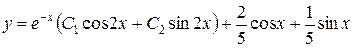Пример 6. Найти общий интеграл линейного неоднородного уравнения .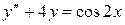

Решение. Характеристическое уравнения 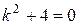имеет корни . Поэтому общий интеграл соответствующего однородного уравнения

.

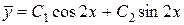Частное решение неоднородного уравнения ищем в форме

.

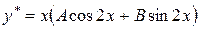Тогда

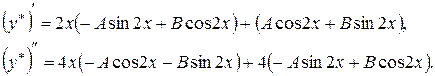
Подставляя эти выражения производных в данное уравнение и приравнивая коэффициенты при cos2x и sin2x, получаем систему уравнений для определения А и В: 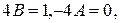откуда .

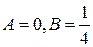Таким образом, общий интеграл данного уравнения

.

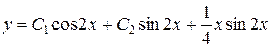Дата добавления: 2014-01-04