
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные трансцендентные функции
|
|
|
|
.
Эти области можно выбирать так, чтобы они, не налегая друг на друга, заполнили собой всю плоскость (как это уже имеет место для указанных областей однолистности  ). Такой выбор произведен на Рис.45.1. Каждая из изображенных здесь областей преобразуется посредством соответствующей функции
). Такой выбор произведен на Рис.45.1. Каждая из изображенных здесь областей преобразуется посредством соответствующей функции  в области, указанные на Рис.44.2. Обратно, если
в области, указанные на Рис.44.2. Обратно, если  изменяется в одной из этих последних областей, то
изменяется в одной из этих последних областей, то  можно считать изменяющимся в любой из соответствующих областей Рис.45.1., благодаря чему можно было бы говорить не об одной, а об
можно считать изменяющимся в любой из соответствующих областей Рис.45.1., благодаря чему можно было бы говорить не об одной, а об 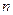 функциях, обратных функции
функциях, обратных функции 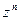 , определённых в области
, определённых в области  , и о бесконечном множестве функций, обратных функциям
, и о бесконечном множестве функций, обратных функциям 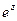 и
и  , определённых в областях
, определённых в областях  и
и  соответственно. Эти функции рассматриваются как различные' ветви, многозначных функций
соответственно. Эти функции рассматриваются как различные' ветви, многозначных функций  , причем первая из этих функций имеет
, причем первая из этих функций имеет 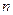 ветвей {
ветвей {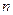 – значная функция), а последние две – бесконечное множество ветвей (бесконечнозначные функции). Чтобы фиксировать какую-либо из ветвей, достаточно лишь указать, в какой из областей Рис.45.1. должно изменяться
– значная функция), а последние две – бесконечное множество ветвей (бесконечнозначные функции). Чтобы фиксировать какую-либо из ветвей, достаточно лишь указать, в какой из областей Рис.45.1. должно изменяться  . В соответствии с обозначениями на этой фигуре мы будем пока пользоваться следующими обозначениями для ветвей наших функций:
. В соответствии с обозначениями на этой фигуре мы будем пока пользоваться следующими обозначениями для ветвей наших функций:

| Рис.45.1.а. | Рис.45.1.б. | Рис.45.1.в. |
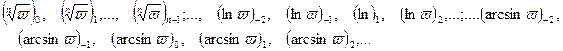
Здесь, например,  обозначает ту ветвь логарифма, значения которой падают внутрь полосы
обозначает ту ветвь логарифма, значения которой падают внутрь полосы 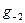 Рис.45.1.б.
Рис.45.1.б.
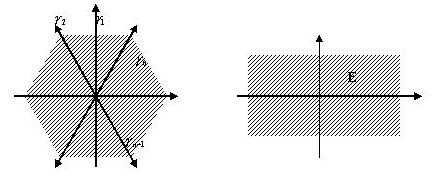
| Рис.45.2.а | Рис.45.2.б. |
Необходимо иметь в виду, что понятие ветви тесно связано с определённым выбором областей однолистности. Так, для функции  можно было бы брать области однолистности:
можно было бы брать области однолистности: 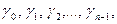 представленные на Рис.45.2. а. Это – углы:
представленные на Рис.45.2. а. Это – углы: 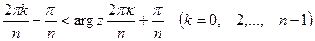 заключённые между биссектрисами углов Рис.45.1.а. Если
заключённые между биссектрисами углов Рис.45.1.а. Если  изменяется в любой из этих областей, то
изменяется в любой из этих областей, то  описывает одну и ту же область
описывает одну и ту же область 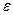 , изображённую на Рис.45.1.б. В самом деле, когда точка
, изображённую на Рис.45.1.б. В самом деле, когда точка  описывает луч
описывает луч  ., то точка
., то точка 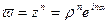 описывает, очевидно, луч
описывает, очевидно, луч  ., и если
., и если 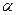 меняется
меняется  , то луч
, то луч 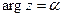 , вращаясь против часовой стрелки, пробегает всю область
, вращаясь против часовой стрелки, пробегает всю область 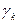 , в то время как соответствующий ему луч
, в то время как соответствующий ему луч 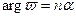 , вращаясь в том же направлении – от луча
, вращаясь в том же направлении – от луча 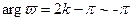 до луча
до луча  пробегает всю область
пробегает всю область 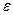 .
.
В области 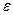 также может быть определена функция, обратная функции
также может быть определена функция, обратная функции  , и притом
, и притом 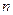 различными способами, сообразно
различными способами, сообразно 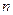 различным областям
различным областям 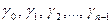 . Иными словами, в области
. Иными словами, в области 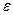 также могут быть определены
также могут быть определены 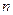 ветвей функции
ветвей функции 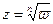 . Если фиксировать одну из областей
. Если фиксировать одну из областей 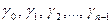 например
например 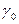 , то мы получим одну определённую ветвь функции
, то мы получим одну определённую ветвь функции 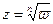 . При этом, когда
. При этом, когда  находится в верхней полуплоскости
находится в верхней полуплоскости 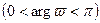 , точка
, точка  будет находиться внутри угла:
будет находиться внутри угла:  , т.е. в части плоскости, принадлежащей как области
, т.е. в части плоскости, принадлежащей как области 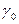 , так и области
, так и области 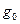 , а когда
, а когда  будет находиться в нижней полуплоскости
будет находиться в нижней полуплоскости  , то точка
, то точка  будет находиться внутри угла:
будет находиться внутри угла: 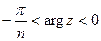 , т. е. в части плоскости
, т. е. в части плоскости  , принадлежащей как области
, принадлежащей как области 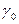 так и области
так и области  .
.
А это значит, что рассматриваемая нами ветвь функции будет в части области 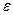 (в верхней полуплоскости) совпадать с ранее определённой ветвью
(в верхней полуплоскости) совпадать с ранее определённой ветвью  , а в другой части области
, а в другой части области 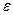 (в нижней полуплоскости) будет совпадать с другой из ранее определённых ветвей, именно с
(в нижней полуплоскости) будет совпадать с другой из ранее определённых ветвей, именно с  . Итак, было бы неправильно рассматривать ветви одной и той же многозначной функции как отдельные функции; в нашем примере при изменившемся выборе областей однолистности две ветви
. Итак, было бы неправильно рассматривать ветви одной и той же многозначной функции как отдельные функции; в нашем примере при изменившемся выборе областей однолистности две ветви  и
и  рассматривавшиеся сначала как различные, определяют одну и ту же ветвь.
рассматривавшиеся сначала как различные, определяют одну и ту же ветвь.
Мы установили наличие различных ветвей функций  ,
, 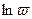 и
и  пользуясь понятием областей однолистности. К тому же результату легко прийти и иным путём. Так, полагая
пользуясь понятием областей однолистности. К тому же результату легко прийти и иным путём. Так, полагая  , выводим последовательно из уравнения
, выводим последовательно из уравнения  :
:
 ,
,
откуда  (имеется в виду арифметическое значение радикала) и
(имеется в виду арифметическое значение радикала) и  . Придавая здесь
. Придавая здесь 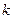 значения
значения 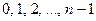 , получим
, получим 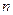 различных значений функции
различных значений функции  , соответствующих
, соответствующих 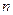 различным ветвям этой многозначной функции:
различным ветвям этой многозначной функции:
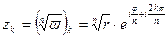
Значения эти имеют один и тот же модуль; аргументыих представляют арифметическую прогрессию с разностью  . Очевидно,чтоточки
. Очевидно,чтоточки  по одной размещаются в областях Рис.45.1.,45.2.а.
по одной размещаются в областях Рис.45.1.,45.2.а.
Фиксируя какое-либо исходное значение радикала 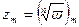 , заставим точку
, заставим точку  в плоскости
в плоскости  описать некоторую замкнутую кривую. Если эта кривая не заключает внутри начала координат, то непрерывно изменяющийся аргумент
описать некоторую замкнутую кривую. Если эта кривая не заключает внутри начала координат, то непрерывно изменяющийся аргумент  вернётся к прежнему значению, когда точка вновь примет исходное положение. Соответственно с этим и значение
вернётся к прежнему значению, когда точка вновь примет исходное положение. Соответственно с этим и значение  останется прежним. Не то будет, если точка в плоскости
останется прежним. Не то будет, если точка в плоскости  опишет замкнутую кривую, заключающую внутри начало координат. После полного обхода аргумент
опишет замкнутую кривую, заключающую внутри начало координат. После полного обхода аргумент  либо увеличится на
либо увеличится на  , когда обход делался против часовой стрелки, либо уменьшится на
, когда обход делался против часовой стрелки, либо уменьшится на  , когда обход делался по часовой стрелке. В соответствии с этим непрерывно меняющееся по мере обхода значение
, когда обход делался по часовой стрелке. В соответствии с этим непрерывно меняющееся по мере обхода значение  в первом случае перейдёт от
в первом случае перейдёт от  , во втором случае от
, во втором случае от 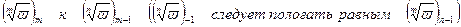 полагать равным
полагать равным  .
.
Повторяя обход, вокруг начала координат в том или в другом направлении достаточное количество раз, мы можем перейти от значения  к любому другому значению радикала в той же точке
к любому другому значению радикала в той же точке 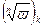 . Точка, обладающая тем свойством, что обход вокруг неё переводит от одной ветви многозначной функции к другой ветви, называется точкой разветвления этой функции (или критической точкой}. Таким образом, точка
. Точка, обладающая тем свойством, что обход вокруг неё переводит от одной ветви многозначной функции к другой ветви, называется точкой разветвления этой функции (или критической точкой}. Таким образом, точка  является точкой разветвления для функции
является точкой разветвления для функции 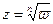 . Так как полный поворот на угол
. Так как полный поворот на угол  около начала координат в то же время является и полным поворотом около бесконечно удалённой точки (для лучшего уяснения этого факта следует вместо плоскости
около начала координат в то же время является и полным поворотом около бесконечно удалённой точки (для лучшего уяснения этого факта следует вместо плоскости  представить себе риманову сферу), то бесконечно удалённая точка также является точкой разветвления функции
представить себе риманову сферу), то бесконечно удалённая точка также является точкой разветвления функции  . Других точек разветвления эта функция не имеет, так как обход в плоскости
. Других точек разветвления эта функция не имеет, так как обход в плоскости  по любой кривой, не заключающей внутри начала координат, не изменяет значения радикала. Заметим, что точка
по любой кривой, не заключающей внутри начала координат, не изменяет значения радикала. Заметим, что точка 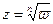 , в то время как точка
, в то время как точка  делает полный оборот около начала координат, описывает незамкнутую дугу, соединяющую точки
делает полный оборот около начала координат, описывает незамкнутую дугу, соединяющую точки 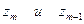 (или
(или  ) двух соседних областей однолистности. Новому обороту (в прежнем направлении) соответствует движениеточки
) двух соседних областей однолистности. Новому обороту (в прежнем направлении) соответствует движениеточки  вдоль новой незамкнутой дуги
вдоль новой незамкнутой дуги  и т. д. После
и т. д. После 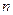 оборотов точки
оборотов точки  около начала координат точка
около начала координат точка  сделает один оборот около начала координат. В случае же, когда точка
сделает один оборот около начала координат. В случае же, когда точка  описывает замкнутую кривую, не содержащую внутри начала координат, то точка
описывает замкнутую кривую, не содержащую внутри начала координат, то точка  описывает также замкнутую кривую, не содержащую внутри начала координат. (На своём пути она может выходить из первоначальной области однолистности и побывать во всех остальных сколько угодно раз; в конце пути она займёт первоначальное положение.)
описывает также замкнутую кривую, не содержащую внутри начала координат. (На своём пути она может выходить из первоначальной области однолистности и побывать во всех остальных сколько угодно раз; в конце пути она займёт первоначальное положение.)
Переходя к функции  , рассмотрим соотношение
, рассмотрим соотношение  . Полагая здесь
. Полагая здесь 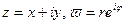 , получаем:
, получаем: 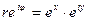 , откуда
, откуда

или 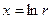 (подразумевается действительное значение логарифма положительного числа
(подразумевается действительное значение логарифма положительного числа 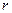 ),
), 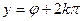 . Таким образом,
. Таким образом,  .
.
Разным значениям 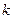 соответствуют разные значения
соответствуют разные значения  , таким образом, мы имеем здесь бесконечное множество разных значений
, таким образом, мы имеем здесь бесконечное множество разных значений 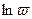 , соответствующих бесчисленным ветвям этой многозначной функции. Значения
, соответствующих бесчисленным ветвям этой многозначной функции. Значения  имеют одну и ту же действительную часть; коэффициенты при
имеют одну и ту же действительную часть; коэффициенты при  образуют арифметическую прогрессию с разностью
образуют арифметическую прогрессию с разностью  . Очевидно, что точки с аффиксами
. Очевидно, что точки с аффиксами  размещаются по одной во всех областях Рис.45.1.б. Фиксируя какое-либо исходное значение
размещаются по одной во всех областях Рис.45.1.б. Фиксируя какое-либо исходное значение 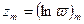 заставим точку плоскости
заставим точку плоскости  описать замкнутую кривую, начальной и исходной точкой которой является
описать замкнутую кривую, начальной и исходной точкой которой является  . Рассуждая, как и выше, придём к заключению, что точка
. Рассуждая, как и выше, придём к заключению, что точка  , а также и точка
, а также и точка 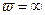 являются точками разветвления функции
являются точками разветвления функции  . Именно, если точка
. Именно, если точка  делает около начала координат
делает около начала координат 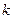 оборотов, то значение
оборотов, то значение 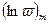 переходит в значение
переходит в значение 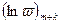 , когда обороты делаются против часовой стрелки, и в значение
, когда обороты делаются против часовой стрелки, и в значение  , когда обороты делаются по часовой стрелке. Таким образом, путём достаточного числа оборотов около начала координат, совершаемых в должном направлении, можно перейти от одного значения логарифма в точке
, когда обороты делаются по часовой стрелке. Таким образом, путём достаточного числа оборотов около начала координат, совершаемых в должном направлении, можно перейти от одного значения логарифма в точке  к любому другому значению в той же точке.
к любому другому значению в той же точке.
Отличие от предыдущего случая заключается в том, что, производя обороты вокруг начала координат в одном и том же направлении, мы никогда не вернёмся к исходному значению, но всегда будем получать новые. Это отличие характеризуют, говоря, что точка  является для функции
является для функции 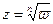 точкой разветвления конечного порядка, а именно порядка
точкой разветвления конечного порядка, а именно порядка  , в то время как для функции
, в то время как для функции  та же точка служит точкой разветвления бесконечного порядка. Говорят также, что в первом случае точка разветвления является алгебраической, а во втором –трансцендентной.
та же точка служит точкой разветвления бесконечного порядка. Говорят также, что в первом случае точка разветвления является алгебраической, а во втором –трансцендентной.
Определение 45.1. Трансцендентными называются аналитические функции, которые не являются алгебраическими.
Если аргументом показательной или тригонометрических функций является комплексное число, то определение этих функций, вводимое в элементарной алгебре теряет смысл.
Рассмотрим разложение в степенной ряд следующих функций:

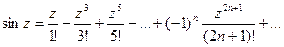
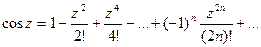
Функции ez, cosz, sinz связаны между собой формулой Эйлера. Эта формула может быть очень легко получена сложением соответствующих рядов.

Также справедливы равенства:
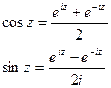
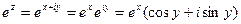
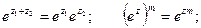
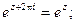

Для тригонометрических функций комплексного аргумента справедливы основные тригонометрические тождества (синус и косинус суммы, разности и т.д.), которые справедливы для функций действительного аргумента.
Определение 45.2. Гиперболическим синусом, косинусом, тангенсом и котангенсом называются соответственно функции:
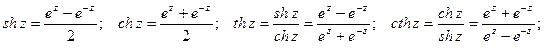
Гиперболические функции могут быть выражены через тригонометрические:
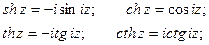
Гиперболические функции sh z и ch z имеют период 2pi, а функции th z и cth z – период pi.
Пример 45.1
Найти sin(1+2i).
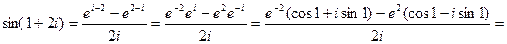

Определение 45.3. Логарифмическая функция комплексного аргумента определяется как функция, обратная показательной.
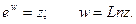
Если w = u + iv, то 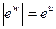 и Arg ew =
и Arg ew =  = v.
= v.
Тогда eu = 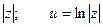 .
.
Итого: 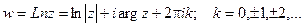
Для комплексного числа z = a + ib 
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1446; Нарушение авторских прав?; Мы поможем в написании вашей работы!