Напряжения и деформации при кручении стержня круглого сечения

Теория кручения стержней круглого поперечного сечения основана на следующих допущениях:

1. Плоские поперечные сечения до закручивания остаются плоскими и после закручивания (гипотеза плоских сечений Бернулли).

2. Радиусы поперечных сечений не искривляются, а только поворачиваются на некоторые углы.

3. Расстояние между поперечными сечениями не изменяются.

Указанные допущения подтверждаются опытами. Возьмем вал и в недеформированном состоянии нанесем сетку:

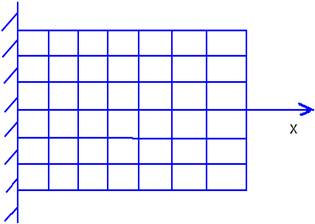Закрутим вал

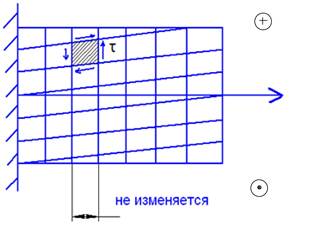
Рассмотрим вал, закрученный внешним крутящим моментом:

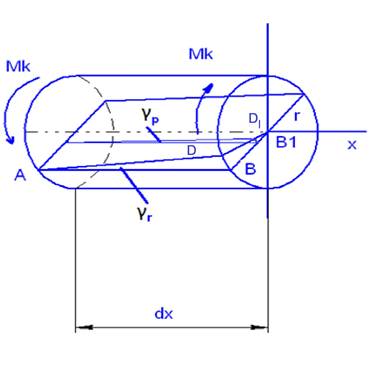Выделим из вала двумя поперечными сечениями элемент длинной dx. Покажем элемент dx в крупоном масштабе. Он уравновешен M_к:

r – наружный радиус

ρ – текущий радиус

γ_r – угол сдвига

АВ – образующая до деформации

Рассмотрим три стороны задачи:

1. Геометрические соотношения

Рассмотрим геометрию деформированного элемента.

BB₁=γ_rdx=rd поделим и получаем (1)

DD₁=γ_ρdx=ρd

Углы сдвигов прямо пропорциональны расстоянию точек до центров тяжести сечения.

2. Физические соотношения

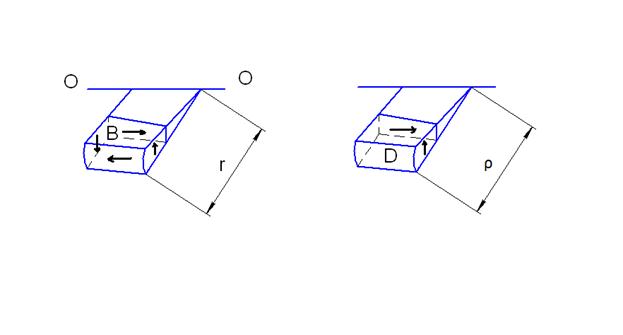Элементы, выделенные в окрестности точек B и D испытывают чистый сдвиг.

Запишем закон Гука при чистом сдвиге для точек B и D.

точка B τ_r=Gγ_r 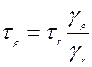(2)

точка D τ_ρ=Gγ_ρ

Учитывая соотношения (1) и (2) окончательно получим:

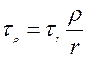(3)

где τ_r – напряжения на контуре.

Согласно зависимости (3) касательные напряжения в поперечных сечениях вала изменяются по линейному закону.

Покажем эпюру касательных напряжений τ._.

Вектор касательных напряжений в точке В направлен в направлении M_k.

3. Статические отношения

Интегральные характеристики мы рассматривали ранее.

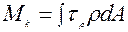, Заменим τ_ρ из соотношения (3)

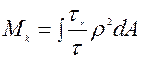. Известно, что 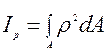-полярный момент инерции сечения.

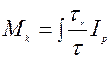
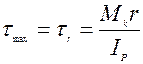(4)

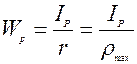- полярный момент сопротивления круглого сечения вала

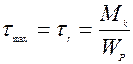
Для определения напряжений в любой точке подставим в (3) значения τ из (4), и получим:

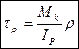(5)

Формула (5) определяет касательные напряжения при кручении вала круглого сечения. Это основная формула для определения τ в любой точке вала.

Установим формулу для определения углов закручивания вала. Введем 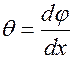– относительный угол закручивания, т.е. угол закручивания единицы длины вала, выраженный в радианах.

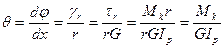
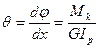(6)

Формула (6) определяет относительный угол закручивания вала.

GI_p – жесткость круглого сечения вала при кручении.

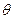– приходится на 1-у единицу вала, а на dx приходится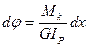

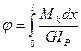(7)

Формула (7) определяет полный угол закручивания вала.

При постоянных M_k и GI_p формула (7) упрощается

(8)

Формула (8) определяет полный угол закручивания при M_k = const, GI_p= const.

Соотношение (8) выражает закон Гука при кручении стержня в развернутой форме, так же как .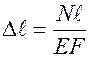

Для ступенчатого вала, при постоянных значениях M_k и GI_p на каждом участке, углы закручивания подсчитываются по участкам по формуле (8) и результаты суммируются

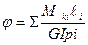, (9)

где i – номер участка.

Дата добавления: 2014-01-04