Цепи Маркова с непрерывным временем

УЧЕБНЫЕ ВОПРОСЫ И РАСЧЕТ ВРЕМЕНИ

Воспитывать творческий подход и настойчивость при изучении дисциплины

Рассмотреть математический аппарат, используемый для конструирования вероятностных моделей ПР.

УЧЕБНЫЕ И ВОСПИТАТЕЛЬНЫЕ ЦЕЛИ

Занятие № 37. Марковские модели принятия решений.

Тема № 8. Вероятностные задачи ТПР.

Теория принятия решений

По учебной дисциплине

ЛЕКЦИЯ

Обсуждено на заседании ПМК

"___" августа 2009 г.

Протокол № 1

1. Изучить основныепонятия и типы вероятностных задач, а также применяемые критерии оценки их решений.

Время: 2 часа. Место: Аудитория.

МАТЕРИАЛЬНОЕ ОБЕСПЕЧЕНИЕ:

Литература : Орлов А.И. Теория принятия решений. Учебник.. М., «Экзамен», 2006.

Наглядные пособия: дидактический материал (слайды).

Технические средства обучения: “Лектор–2000”.

I.	Введение		мин.
II.	Учебные вопросы
	1. Цепи Маркова с непрерывным временем.		мин.
	2. Основные понятия и компоненты систем массового обслуживания.		мин.
	3. Вероятностные характеристики наиболее распространенных потоков событий		мин.
III.	Заключение		мин.

ВВЕДЕНИЕ

Проверить наличие студентов и их готовность к занятию.

Объявить студентам о том, что они продолжают изучение темы «Вероятностные задачи ТПР», играющей важнейшую роль в теории принятия решений. Довести до студентов, что данная тема включает 9 часов аудиторных занятий, из которых 4 часа лекций, 5 часа практических занятий.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ИЗЛОЖЕНИЮ УЧЕБНЫХ ВОПРОСОВ

При изложении первого вопроса изучить цепи Маркова с непрерывным временем. Изложение учебного материала проводится с элементами диалогового метода, при этом студентам задается следующий вопрос: ´ Какая матрица называется инфинитезимальной?

При изложении второго вопроса рассмотреть основные понятия и компоненты систем массового обслуживания. Изложение учебного материала проводится с элементами диалогового метода, при этом студентам задается следующий вопрос: ´ Назовите основные компоненты СМО.

При изложении третьего вопроса рассмотреть вероятностные характеристики наиболее распространенных потоков событий. Изложение учебного материала проводится с элементами диалогового метода, при этом студентам задается следующий вопрос: ´ Какой поток называется эрланговским?

Этот класс случайных процессов характеризуется тем, что переходы осуществляются за бесконечно малый интервал времени Δt и известной являет­ся λ_ij - интенсивность перехода из i -го в j -е состояние:

,

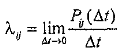где P_ij(Δt) — вероятность перехода из i -ro в j -е состояние за бесконечно малый промежуток времени Δt.

Для описания таких цепей Маркова используется стандартная схема, в которой:

каждое состояние представляется в виде вершины графа;

между вершинами указываются дуги, отражающие возможность перехо­да системы из i -го состояния в j -е за бесконечно малый интервал Δt;

над дугами проставляются величины интенсивностей переходов λ_ij. Такой граф называется размеченным, и на основе этого графа конструируются следующие соотношения:

система дифференциальных уравнений для исследования переходных режимов, протекающих в анализируемой системе;

система алгебраических уравнений для вычисления компонент вектора распределения стационарных вероятностей.

Пример. Предположим, что задан размеченный граф, содержащий четыре состояния: S₁, S₂, S₃, S₄, и определены интенсивности переходов между состояниями: λ₁₂, λ₂₄, λ₄₁, λ₃₄, λ₂₃ (рис. 1). Необходимо вывести дифференциальное уравнение, позволяющее исследовать динами­ку изменения вероятностей для каждого из состояний.

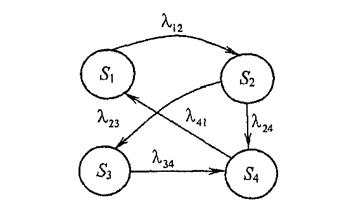
Рис. 1

Рассмотрим вывод уравнения для состояния S₄:

,

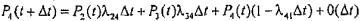где P₄(t+Δt) - вероятность того, что процесс в момент времени t+Δt находится в состоянии S₄;

Р₂(t), Р₃(t), P₄(t) - соответственно вероятности того, что в момент времени t процесс находится в состояниях S₂, S₃, и S₄;

λ₂₄ Δt - вероятность перехода из состояния S₂ в состояние S₄ за время Δt с точностью до бесконечно малой величины;

λ₃₄ Δt - вероятность перехода из состояния S₃ в состояние S₄ за время Δt;

( 1- λ₄₁ Δt) - вероятность того, что процесс не перейдет из состояния S₄ в состояние S₁, за бесконечно малый интервал времени Δt.

Над полученным уравнением выполняются следующие преобразования: раскрытие ско­бок; перенос переменной P₄(t) из левой части в правую; деление правой и левой частей на вели­чину Δt и взятие предела по Δt => 0. Тогда

.

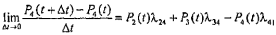Очевидно, что левая часть представляет собой производную от P₄(t) по времени. Окон­чательно,

.

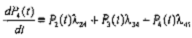На основе полученного уравнения для состояний S₄, предлагается сле­дующая процедура составления дифференциальных уравнений:

дифференциальное уравнение составляется для каждого из состояний размеченного графа:

предположим, что составляется уравнение для состояния S_i. Тогда в левой части указывается производная от вероятности i -го состояния

,

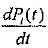а в правой части записывается алгебраическая сумма произведений интенсивно­сти перехода на вероятность соответствующего состояния, причем со знаком минус берутся произведения вероятности рассматриваемого i -го состояния P_i(t) на интенсивность перехода из i -го состояния в другие состояния λ_ij, а со знаком плюс берутся произведения вероятностей других j -х состояний на интенсив­ность перехода из другого j -го состояния в рассматриваемое i-e состояние λ_ji.

Тогда для остальных состояний размеченного графа состояний дифференциальные урав­нения имеют следующий вид:

для

;

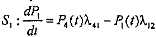для

;

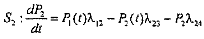для

.

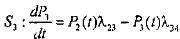Решение полученной системы дифференциальных уравнений необходимо выполнить с учетом уравнения нормировки:

.

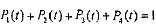При стремлении t к бесконечности процесс переходит в установившийся режим, для ко­торого можно найти стационарные вероятности

.

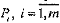Стационарная вероятность для состоя­ния S_i представляет собой долю времени, которую пребывает процесс в этом состоянии. В устано­вившемся режиме

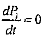
и в результате получается система алгебраических уравнений:

,

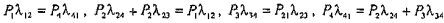где Р₁, Р₂, Р₃, Р₄ - вероятности стационарных состояний.

Общее правило составления алгебраических уравнений для стационарных вероятностей включает выполнение следующих шагов:

алгебраические уравнения составляются для каждого состояния;

предположим, что рассматривается состояние S_i. В левой части уравне­ния указывается сумма произведений λ_iℓ интенсивности перехода из i -го состояния в другое ℓ -е состояние на вероятность i -го состояния P_i, а в правой части - сумма произведений интенсивности перехода из другого j -го состояния в i- e состояние λ_ji на вероятность j -го состояния P_j.

Необходимо отметить, что составление системы алгебраических уравне­ний для сложных по структуре размеченных графов представляет существенные трудности. Современный подход к вычислению стационарных вероятностей ос­нован на использовании, так называемых, инфииитезимальных матриц:

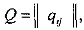
где q_ij вычисляется следующим образом:

q_ij = λ_ij, если

,

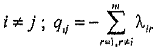если

.

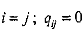в остальных случаях.

Для рассматриваемого графа:

.

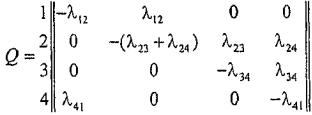Вектор стационарного распределения вероятностей

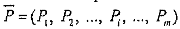
находится из решения системы уравнений:

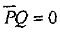
с учетом условия нормировки

.

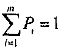Для приведения полученной системы линейных уравнений к канониче­скому виду Ах=В используется соотношение (PQ)^T = Q^TP^T = 0.

Для введения в систему уравнений условия нормировки элементы первой строки матрицы Q^T полагаются равными единице, и формируется столбец сво­бодных чисел В, первый элемент которого равен единице, а остальные элемен­ты - нулю. Тогда матрица А имеет вид:

.

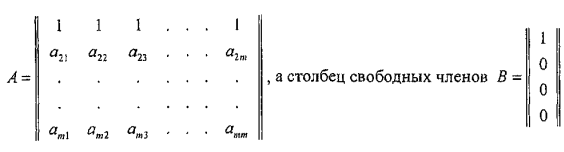Необходимо отметить, что наибольший эффект от применения инфинитезимальных матриц достигается в том случае, если для исследуемого графа состояний возможно конструирование алгоритма формирования элементов мат­рицы q_ij. Очевидно, что при большой размерности графа, ручное заполнение матрицы Q представляет определенные сложности.

Предположим, что имеется граф состояний, описывающий процесс гибе­ли и размножения (рис. 2).

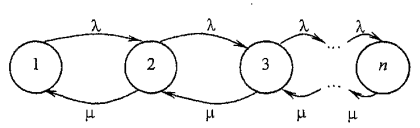
Рис. 2. Размеченный граф состояний для процесса гибели и размножения

Тогда

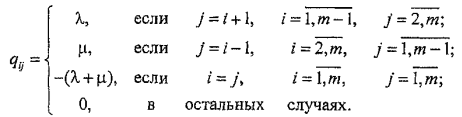
Дата добавления: 2014-01-04