Учение о Боге

.

Для нахождения собственно плотности распределения для закона Эрлан­га k- го порядка необходимо использовать оператор обратного преобразования:

.

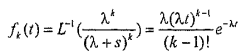Количественные характеристики закона Эрланга. Математическое ожи­дание длительности интервала между соседними событиями находится как сум­ма математических ожиданий для длительности интервала между событиями в порождающем пуассоновском потоке:

,

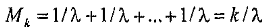где 1/λ, - средняя длительность интервала между событиями в пуассоновском потоке.

Интенсивность эрланговского потока событий обратно пропорциональна математическому ожиданию:

.

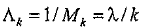Дисперсия для закона Эрланга k- го порядка определяется как сумма дис­персий для пуассоновского потока. Такая процедура правомерна, т.к. суммируе­мые случайные величины являются независимыми

.

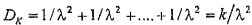Среднеквадратичное отклонение находится как:

.

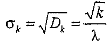Целесообразно вычислить среднеквадратичное отклонение σ_k, через интенсивность эрланговского потока

.

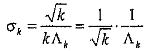Полученное соотношение определяет основное свойство закона Эрланга, которое состоит в том, что путем изменения порядка закона k можно описать весь спектр потоков событий от самого случайного, к которому отно­сится пуассоновский поток событий, до самого неслучайного. Таким неслучай­ным потоком является детерминированный поток, в котором наступление собы­тий производится в строго определенные моменты времени. Очевидно, что если сохранить в потоке событий постоянным значение средней длительности интер­вала между событиями, т.е. 1/ Λ_k = const, то при k = 1 получается пуассоновский поток с плотностью f(t) = λе^-λt, а при k =>∞ и сохранении 1/ Λ_k =const сред­неквадратичное отклонение σ_k становится равным нулю. Но такими параметра­ми обладает детерминированный поток с плотностью

,

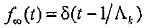где δ(t -1/ Λ_k) -дельта-функция.

ЗАКЛЮЧЕНИЕ

Кратко подводятся итоги занятия, при этом обращается внимание студентов на цели и содержание дисциплины.

Дать задание на самостоятельную работу (отводимое время 4 часа):

ó с целью более глубокого освоения материала повторить и более подробно изучить линейную оптимизацию. Литература: [2] с. 175…190, конспект лекций,

При необходимости ответить на возникшие вопросы.

Старший преподаватель кафедры программного обеспечения И.Денисова

Бог – высшая истина и подлинное бытие, «ибо то только действительно существует, что пребывает неизменно».

Идея троичности бытия.
Бог христианской религии.
«Воля Бога принадлежит к самой сущности божественной»
«Бог – создатель мира, сотворённого из ничего».
Доказательство от противного:
предположим, мир не создан из ничего, тогда мы должны признавать вечную материю. Приходим к противоречию: «Существованием такой материи ограничивалось бы божественное всемогущество».

Если Бог – вечное начало, то не может быть ничего, совечного ему. Следовательно, материя создана.

Концепция непрерывного творения.
Творение мира неверно понимать таким образом, что Бог создал мир в законченном варианте и устранился от него. Бог постоянно поддерживает существование мира своей творческой активностью.
«Если Бог хотя бы на мгновение отнимет от вещей свою производительную силу, то их так же не будет, как не было прежде, чем они были созданы».

Дата добавления: 2014-01-04