Эрланговский поток событий

Эрланговские потоки позволяют с высокой степенью точности описать поступление заявок в реальных системах обслуживания.

Определение 1. Эрланговский поток событий - это последователь­ность заявок, получаемая из пуассоновского потока путем применения опера­ции просеивания.

Таким образом, для формирования эрланговского потока необходимо иметь исходный или порождающий пуассоновский поток событий и указать порядок закона Эрланга k. Предположим, что порядок закона k =3. Тогда из ис­ходного потока выбирается каждое третье событие, и формируется поток Эрланга третьего порядка (рис. 9). Суть операции просеивания состоит в выборе каждого k- го события из порождающего пуассоновского потока.

Определим Т_k - длительность интервала между соседними событиями для потока Эрланга k- го порядка. Предположим, что τ_i, - длительность интерва­ла между i -м и i -1-м событиями в исходном пуассоновском потоке τ_i=t_i - t_i-1, где t_i и t_i-1 - соответственно моменты поступления i -го и i- 1-го событий в исходном потоке. Очевидно, что

.

Рис.9

Случайная величина τ_i, распределена по экспоненциальному закону с плотностью f(t) = λе^-λt, λ=m^-1, где m_i, - средняя длина интервала между соседними событиями в пуассоновском потоке событий.

Для нахождения f_k(t) плотности распределения случайной величины Т_k используется известное соотношение, заключающее в том, что при суммирова­нии случайных величин необходимо перемножить преобразования Лапласа-Стилтьеса для плотностей распределения этих случайных величин. В частности, при суммировании двух случайных величин х и у с известными плотностями распределений f(x) и φ(у) необходимо предварительно определить преобразо­вания Лапласа-Стилтьеса для плотностей распределения

.

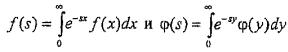Тогда преобразование Лапласа-Стилтьеса q(s) для плотности распреде­ления случайной величины z = х + у представляется, как q(s) = f(s)φ(s), а соб­ственно плотность q(z) случайной величины z находится из обратного преобра­зования q(z)-L^-1(q(s)).

Следовательно, для случайной величины τ_i с известной плотностью рас­пределения f(t) = λе^-λt необходимо определить преобразование Лапласа-Стилтьеса:

.

Так как все τ_i, имеют одинаковую плотность распределения, то преобра­зование Лапласа-Стилтьеса для плотности распределения случайной величины, распределенной по закону Эрланга, представляется следующим образом:

Дата добавления: 2014-01-04