Вероятностные характеристики наиболее распространенных потоков событий

Для формального определения потока событий целесообразно привести ряд определений.

Определение 1. Поток событий { t_k, k > 1 } на интервале времени [0, ∞] представляет, собой неубывающую последовательность случайных мо­ментов t₁, t₂, t₃, …, t_k,..., поступления заявок в систему (рис. 6).

Рис.6

Поток событий по существу представляет случайный процесс x(t), при­нимающий целочисленные значения, равные числу заявок, поступивших за ин­тервал времени [0, t ].

Существуют два способа задания потока событий:

первый способ предполагает задание совместной функции распреде­ления для интервалов времени между соседними моментами поступления заявок τ_i:

;

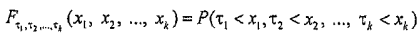второй способ связан с заданием совместного закона распределения для числа заявок, поступивших в различные интервалы времени. Для этого необходимо задать интервалы времени:

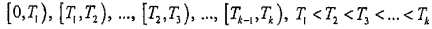
и определить числа x_i, - это количество заявок, поступивших в интервале

.

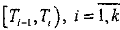Тогда совместный закон распределения

.

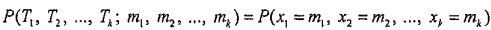Определение 2. Простейший поток - это поток событий, обладаю­щий такими свойствами, как ординарность, стационарность, отсутствие после­действия.

Ординарность состоит в том, что вероятность поступления двух зая­вок за бесконечно малый промежуток времени Δt стремится к нулю, т.е

.

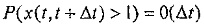Стационарность характеризует неизменность его свойств во време­ни и определяется тем, что количество заявок потока, поступивших в интервале
времени [ Т_i-1, Т_i:), не зависит от расположения этого интервала на временной
оси, а зависит от длительности этого интервала. Отсутствие последействия состоит в том, что количество заявок потока, поступивших в интервале
[ Т_i-1, Т_i:), не зависит от количества заявок, поступивших в интервале времени
[ Т_i, Т_i+1:). Иначе отсутствие последействия отражает независимость случайных величин х₁, х₂,..., х_i,..., х_k, …,(рис. 7).

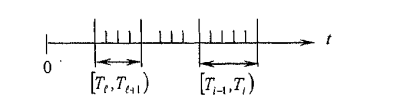
Рис.7

Для простейшего потока событий справедлива следующая формула:

,

где P_n(Т) - вероятность того, что за время t наступит n событий; λ - интенсив­ность потока или количество заявок, поступающих в единицу времени λ = N/T; N - число заявок; T - интервал времени.

За время Г можег поступить от 0 до ∞ заявок, т.е. 0 < п < ∞.

Покажем, что следующий перечень событий:

за время Т не наступает ни одного события;

за время Т наступает одно событие;

за время Т наступает два события;

за время Т наступит бесконечное число событий - образуют полную группу событий.

Для этого необходимо доказать, что

.

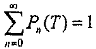Очевидно, что

.

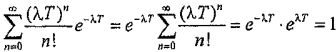Определим математическое ожидание количества событий за время Т, т.е. среднее число событий:

Таким образом, М = λТ.

Другой способ вычисления среднего числа события для пуассоновского потока событий основан на использовании аппарата производящих функ­ций.

Если задана последовательность Р₁,..., Р_n,..., то производящей

функцией P(z) является:

,

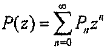где z - комплексная переменная.

Тогда

.

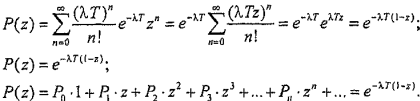
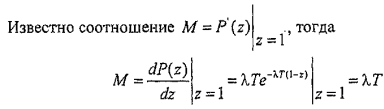Определим выражение для плотности распределения длительности интервала между соседними событиями в простейшем потоке событий (рис. 8).

Рис.8

Все случайные величины τ_i, имеют одинаковую плотность распределе­ния. Найдем функцию распределения для случайной величины τ:

,

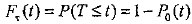где P₀(t) - вероятность того, что за время t не произойдет ни одного события;

1 - P₀(t) - вероятность того, что за время t произойдет хотя бы одно событие.

Подставляя в выражение для пуассоновского потока n= 0, получим

,

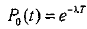тогда

.

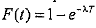Плотность распределения длительности интервала между соседними событиями:

.

Средняя длительность интервала между соседними событиями или мате­матическое ожидание случайной величины τ может быть определено с помощью аппарата преобразования Лапласа-Стилтьеса. Известно, что преобразование Лапласа-Стилтьеса f(s) для плотности распределения вероятности f(t) определяется как

,

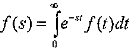где s - комплексная переменная.

Математическое ожидание вычисляется следующим образом:

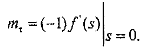
Используя приведенные соотношения для экспоненциальной плотности распределения f(t) = λе^-λt, получим

.

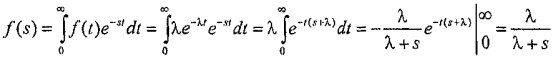Тогда математическое ожидание:

.

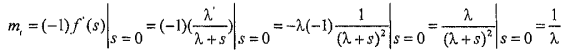Пуассоновский поток событий обладает свойствами суперпозиции и раз­ряжения. Свойство разряжения справедливо для пуассоновского потока с интенсивностью λ, в котором с вероятностью δ_k генерируются заявки k- го типа,

,

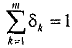и состоит в том, что поток заявок k- го типа также является пуассоновским с интенсивностью δ_kλ. Свойство суперпозиции справедливо для интегрированного потока, состоящего из k пуассоновских потоков с интенсивностями λ_k, k = 1,т, и заключается в том, что интегрированный поток также имеет пуассоновское распределение с интенсивностью

.

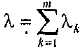Дополнительно, вероятность того, что текущая заявка относится к пуассоновскому потоку k- го типа, равна λ_k/λ. Учитывая, что в потоке Пуассона длительность интервала между соседними событиями распределена по экспоненциальному закону F(t) = 1- е^-λt, то вероятность того, что за бесконечно малое время Δt поступит одна заявка

.

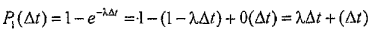Дата добавления: 2014-01-04