
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Признаки сравнения
|
|
|
|
Достаточные признаки сходимости знакопостоянных рядов.
Определение: Знакопостоянный ряд – это такой ряд, все члены которого либо только положительные, либо только отрицательные числа.
При рассмотрении таких рядов достаточно рассмотреть только знакоположительные ряды, так как знак не влияет на вопрос о сходимости ряда.
Пусть даны два знакоположительных ряда: 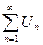 и
и 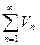 , где
, где 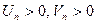 при всех n.
при всех n.
Теорема 1: Если все члены первого ряда не превосходят соответствующих членов второго ряда: 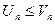 , то если сходится второй ряд, то сходится и первый.
, то если сходится второй ряд, то сходится и первый.
Теорема 2: Если все члены первого ряда не меньше соответствующих членов второго ряда: 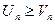 , то если расходится второй ряд, то расходится и первый.
, то если расходится второй ряд, то расходится и первый.
Теорема 3. Если 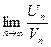 существует и конечен и отличен от нуля, то оба ряда в отношении сходимости ведут себя одинаково.
существует и конечен и отличен от нуля, то оба ряда в отношении сходимости ведут себя одинаково.
В качестве ряда сравнения как правило берут:
| Сходящиеся ряды | Расходящиеся ряды |
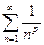 , р>1 – обобщённый гармонический ряд , р>1 – обобщённый гармонический ряд
| 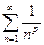 , 0<р<1 , 0<р<1
|
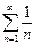 - простой гармонический ряд - простой гармонический ряд
| |
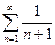 - остаток гармонического ряда - остаток гармонического ряда
| |
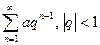 - ряд геометрической прогрессии - ряд геометрической прогрессии
| 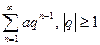
|
Признак Даламбера. Если у знакоположительного ряда 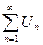 существует и конечен
существует и конечен 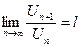 , то если
, то если 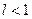 , ряд сходится, если
, ряд сходится, если 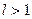 - расходится.
- расходится.
ПРИ 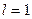 ПРИЗНАК НЕ ДАЁТ ОТВЕТА НА ВОПРОС О СХОДИМОСТИ РЯДА.
ПРИЗНАК НЕ ДАЁТ ОТВЕТА НА ВОПРОС О СХОДИМОСТИ РЯДА.
Признак используют если 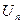 содержит
содержит 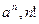 или их вариации.
или их вариации.
Радикальный признак Коши. Если у знакоположительного ряда 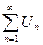 существует и конечен,
существует и конечен, 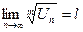 то если
то если 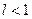 , ряд сходится, если
, ряд сходится, если 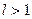 - расходится.
- расходится.
Признак используют если 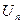 целиком является n – ой степенью некоторого выражения.
целиком является n – ой степенью некоторого выражения.
Интегральный признак Коши. Если функция 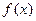 непрерывная, положительная, убывающая при
непрерывная, положительная, убывающая при 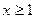 и
и 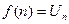 , то ряд
, то ряд 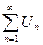 и несобственный интеграл
и несобственный интеграл  одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
Признак используют если 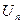 порождает функцию
порождает функцию 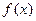 от которой можно без труда найти первообразную.
от которой можно без труда найти первообразную.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 306; Нарушение авторских прав?; Мы поможем в написании вашей работы!